Table of Contents

In this lesson, we research the core of Symmetric Key Algorithms, a fundamental aspect of modern digital security. As we increasingly rely on digital platforms for communication, banking, and data storage, understanding these encryption methods becomes essential. We will explore key algorithms like RC4, ChaCha20, DES, and AES, each significant in safeguarding digital information.
Our focus will be on how these algorithms function, their evolution over time, and their role in protecting data against unauthorized access. The lesson is structured to provide a clear understanding of different cryptographic techniques, highlighting their strengths, limitations, and applications in various scenarios.
Expect a straightforward, insightful journey, tailored for learners from diverse backgrounds. By the end of this lesson, you’ll have a solid grasp of the principles and practices that underpin data security.
Rivest Cipher 4 (RC4)
Rivest Cipher 4, commonly known as RC4, is a stream cipher, a type of symmetric algorithm. It’s renowned for its simplicity and speed in operations. RC4 works by encrypting data one byte at a time. This characteristic makes it particularly useful in applications where data sizes are unknown or vary, such as in secure web communications.
RC4 was designed by Ron Rivest of RSA Security in 1987. Initially, it was a trade secret, but in 1994, its algorithm was anonymously leaked on the internet, leading to its widespread adoption and analysis in the cryptographic community.
The technical workings of RC4 involve a combination of initialization and processing steps. It uses a variable-length secret key (encryption key), typically between 40 and 2048 bits, making it flexible in terms of security strength.
Let us explore the process in more detail:
Step 1: Initialization
RC4 begins with an initialization process known as the Key Scheduling Algorithm (KSA). During this phase, RC4 initializes a 256-byte array which is filled sequentially from 0000 0000 to 1111 1111, often referred to as the State Array.
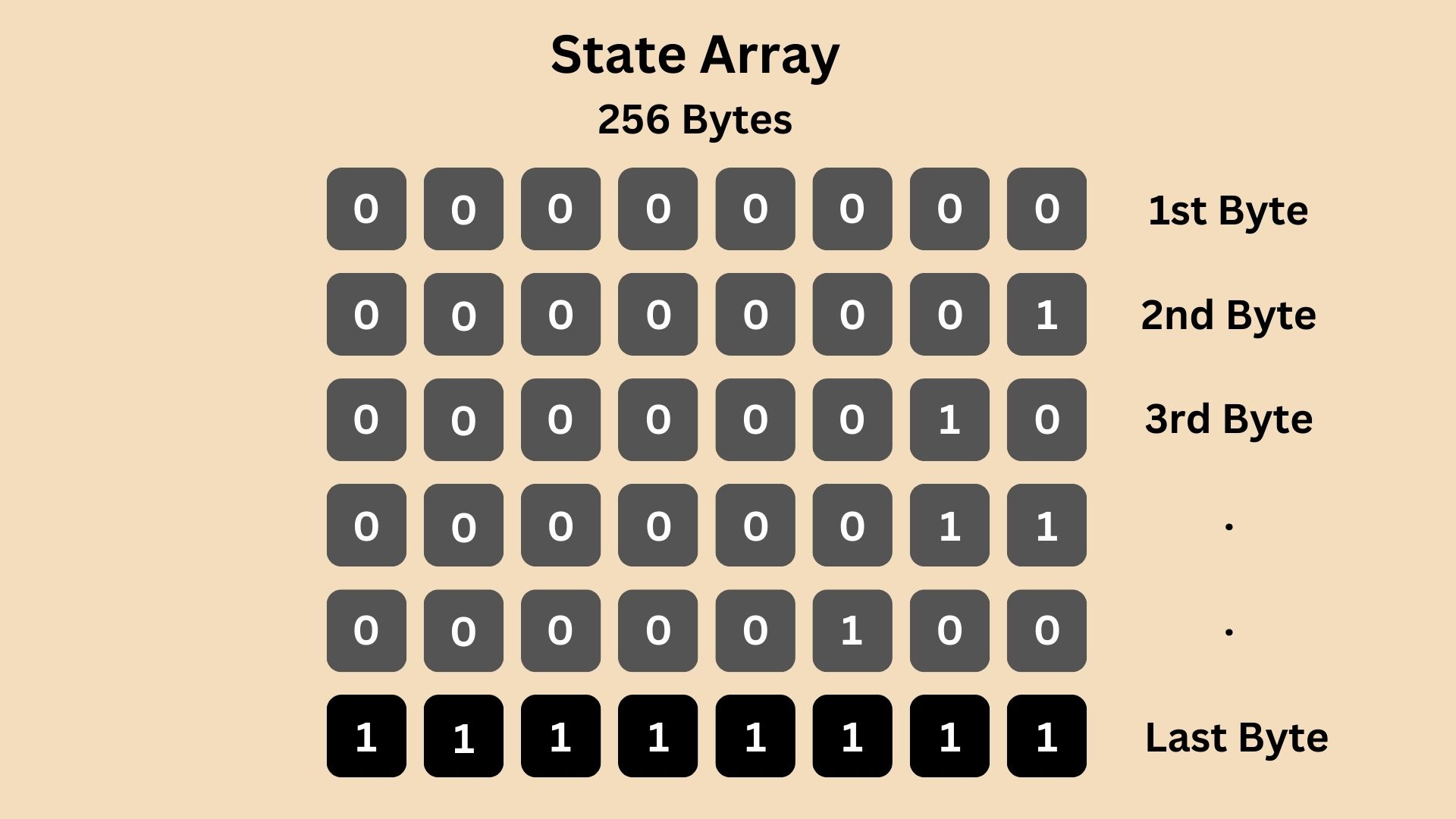
Then, this state array is shuffled using the provided secret key (encryption key) in a process that ensures even a small change in the key will significantly alter the array. This would become something like:
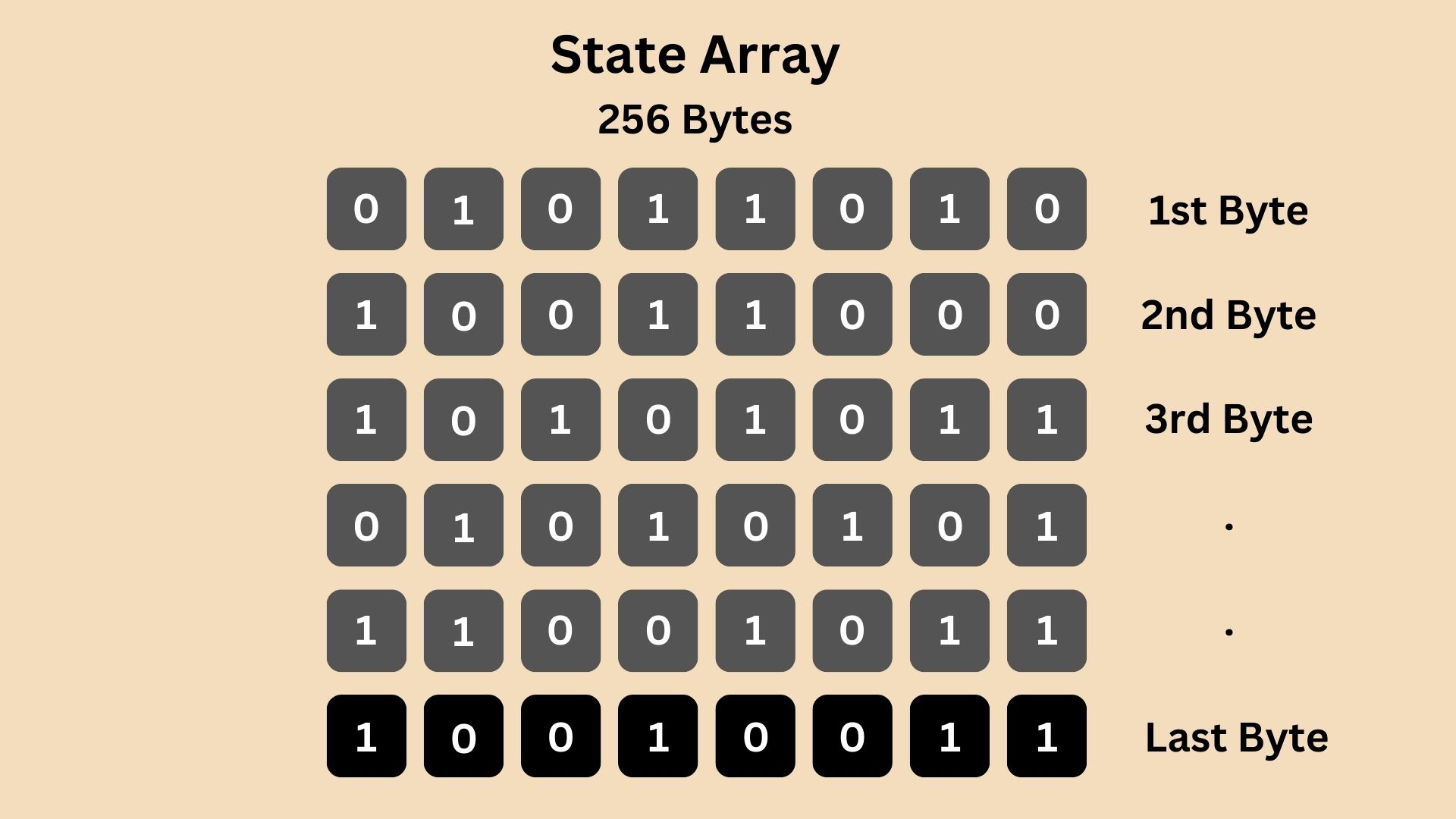
Step 2: Stream Generation
After the Key Scheduling Algorithm (KSA) has shuffled the state array using the secret key, RC4 moves to the Pseudo-Random Generation Algorithm (PRGA) phase. Here, the algorithm uses the shuffled state array to generate a pseudo-random stream of bytes which will be then used to XOR it with the plaintext to generate the final ciphertext. This is done by performing specific operations on the state array:
- Two indices (let’s call them i and j) are initialized to zero.
- In each step of PRGA, the value of i is incremented.
- The value of j is altered based on the current value of j, the value of i, and the state array’s value at the i-th position.
- The algorithm then swaps the values in the state array at positions i and j.
- A pseudo-random byte is generated by selecting a value from the state array at a position determined by adding the values at positions i and j in the array.
- This byte becomes part of the stream used for encryption.
Below is a sample Python code illustrating the PRGA implementation. This code generates a stream of pseudo-random bytes based on the provided state array. In the example given, the first 10 pseudo-random bytes generated by this algorithm are: [2, 5, 7, 13, 13, 23, 31, 40, 40, 56].
def PRGA(state_array):
"""
Pseudo-Random Generation Algorithm (PRGA).
Args:
state_array (list): The state array used for generating the pseudo-random stream.
Returns:
generator: A generator that yields pseudo-random bytes.
"""
i = j = 0
n = len(state_array)
while True:
i = (i + 1) % n
j = (j + state_array[i]) % n
# Swap values in the state array
state_array[i], state_array[j] = state_array[j], state_array[i]
# Generate pseudo-random byte
K = state_array[(state_array[i] + state_array[j]) % n]
yield K
# Example usage
state_array = [i for i in range(256)] # Example state array initialization
prga_generator = PRGA(state_array)
# Generate first 10 pseudo-random bytes
first_10_bytes = [next(prga_generator) for _ in range(10)]
first_10_bytes
Remember, the effectiveness and security of this PRGA depend on the proper initialization of the state array, which is often done as explained using Key Scheduling Algorithm (KSA). Also, the security of the generated stream is highly dependent on the secrecy and randomness of the key used in the initial state setup.
The shuffled state array is used as an input in PRGA algorithm.
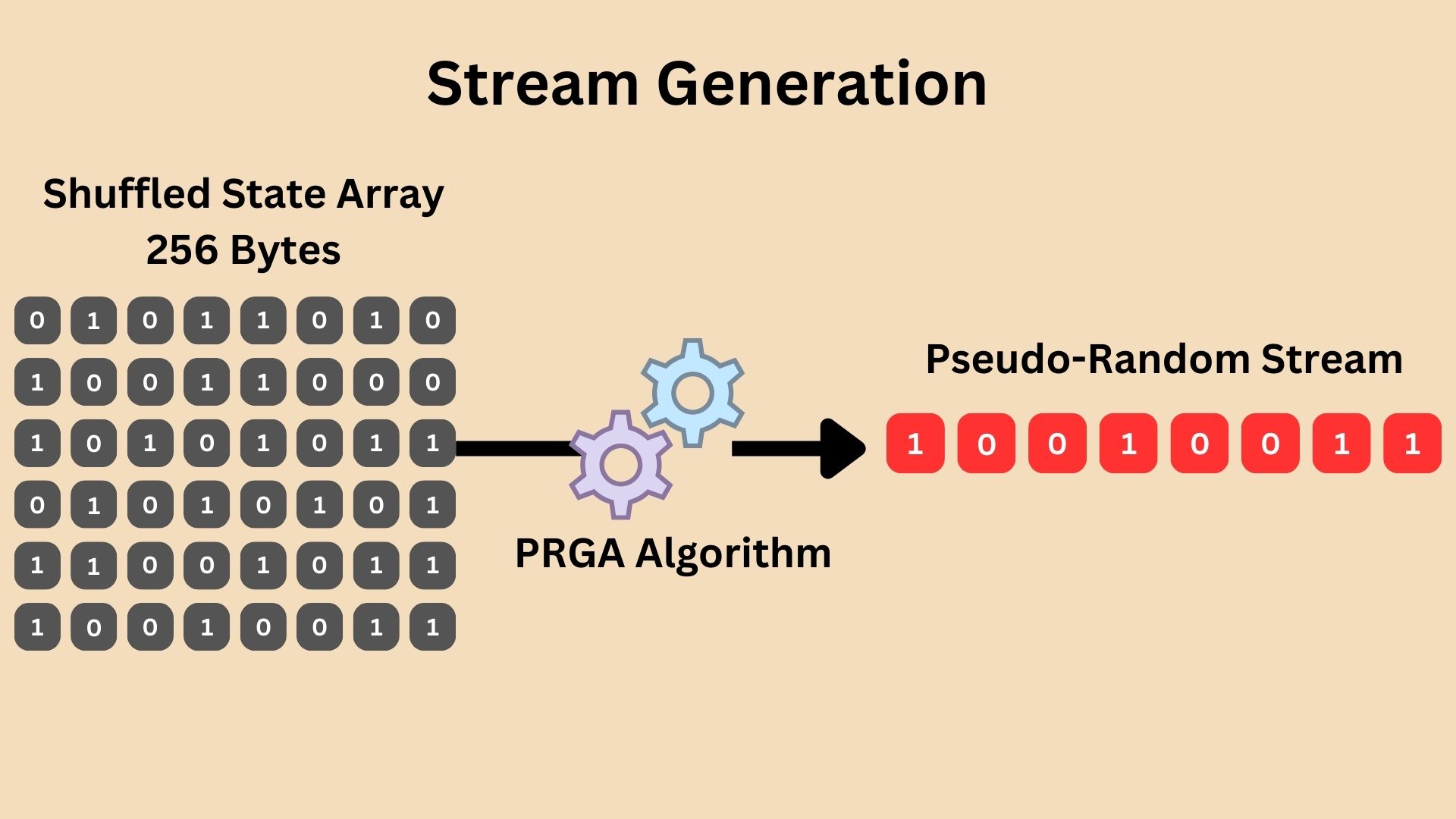
The PRGA essentially cycles through the state array, continuously shuffling it further while extracting bytes that appear random. These bytes are XORed with the plaintext bytes, producing the ciphertext. The continuous evolution of the state array during PRGA ensures that the byte stream is seemingly random and unique for each encryption, directly influenced by the initial shuffling from the secret key.
PRGA generates a byte stream instead of a bit stream for efficiency. Working with bytes (8 bits) aligns better with modern computer architectures, which are optimized for byte-level operations. This alignment enhances performance and simplifies integration with systems that commonly process data in byte-sized chunks.
Step 3: Encryption and Decryption
In the RC4 encryption process, each byte of the plaintext is XOR-ed (Exclusive OR operation) with a corresponding byte from the pseudo-random stream generated by the PRGA. This bitwise operation produces the ciphertext.
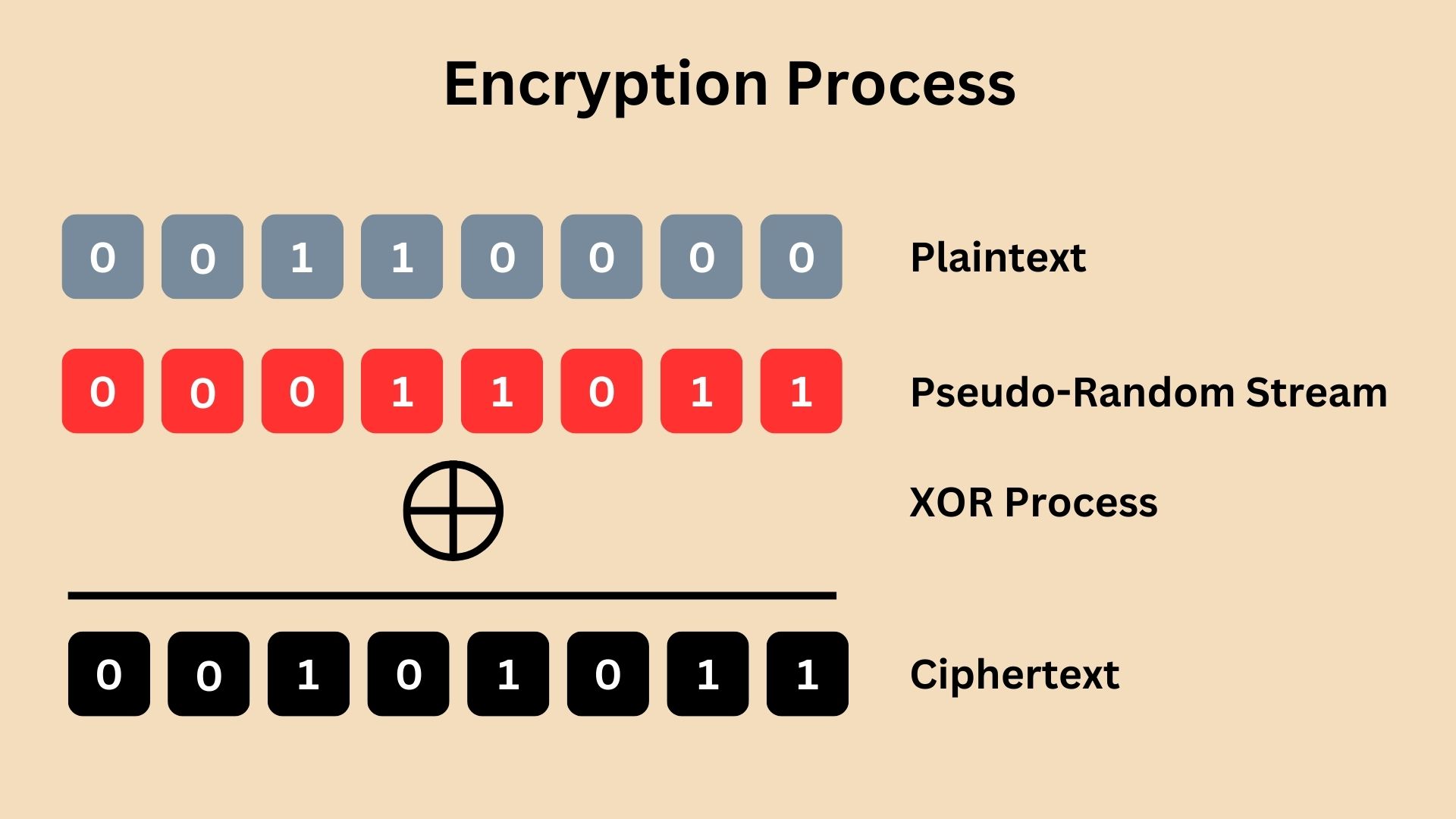
Since the process is symmetrical, decryption in RC4 is identical to encryption. The receiver, using the same secret key, generates the identical pseudo-random stream and XORs it with the ciphertext, resulting in the original plaintext.
The XOR operation in RC4 encryption occurs once for each byte of the plaintext. However, the security doesn’t come from the XOR operation itself, but from the pseudo-random byte stream used in the XOR process. This stream is unique for each encryption, generated based on a secret key. A hacker without the secret key cannot predict this stream. Therefore, simply applying a reverse XOR will not reveal the plaintext without the correct pseudo-random stream derived from the secret key. The pseudo-random byte stream generated by RC4’s PRGA must be kept secret. It’s derived from the secret key and is crucial for ensuring the security of the encrypted data.
The RC4 cipher’s Pseudo-Random Generation Algorithm (PRGA) can potentially repeat the same byte sequence in the generated pseudo-random stream, especially with longer messages. While the initial state array in RC4 is a fixed sequence of 256 bytes, the PRGA modifies this array as it generates each byte, influenced by internal indices. Over a long message, the likelihood of repeating sequences increases. This repetition doesn’t happen in a simple, predictable manner, but the possibility exists. Such repetition can introduce vulnerabilities, as it might give clues to attackers about the encrypted content or the key used.
While RC4 was once a staple in cryptographic protocols, notably in protocols like WEP (Wireless Equivalent Privacy) and SSL/TLS (Secure Sockets Layer/Transport Layer Security), its reliability today is questionable. Over time, vulnerabilities have been discovered, including biases in the pseudo-random stream which can be exploited to recover plaintext from the ciphertext. These vulnerabilities are significant enough that major browsers and online platforms have phased out RC4 support.
Below are the key weaknesses in the RC4 Encryption Algorithm:
- Biases in the Keystream
RC4 generates a keystream with detectable biases (predictable patterns). Certain bytes are more likely to appear in particular positions of the output stream, making it vulnerable to statistical analysis. - Weak Key Initialization
The Key Scheduling Algorithm (KSA) of RC4 can lead to weak initial states for certain keys, making them susceptible to attacks. For example, keys with repeated patterns can produce a non-random initial permutation of the state array, which attackers can exploit to deduce information about the key or plaintext. - Insecure for Short Packets
RC4 is particularly weak in encrypting short packets, as initial bytes of the keystream are more predictable due to biases inherent in the algorithm. In contrast, for longer data streams, the impact of these biases is more diluted because RC4’s keystream becomes less significant relative to the overall data. This makes the patterns less discernible and the encryption relatively stronger. - Vulnerabilities in Protocols
RC4 has been exploited in widely-used protocols. For instance, attacks like BEAST and RC4 NOMORE target weaknesses in RC4 as implemented in TLS and WEP/WPA. - Lack of Authentication
RC4 does not inherently provide authentication like verifying data integrity and origin by leveraging mechanisms such as Hash-based Message Authentication Code (HMAC), making it vulnerable to tampering and forgery attacks.
The “4” in RC4 doesn’t signify a version number or a sequence in a series of ciphers, as one might initially think. Instead, it’s simply part of the name given by its creator, the number 4 was arbitrarily chosen. It doesn’t indicate that there are predecessors like RC1, RC2, or successors like RC5, RC6 in the specific context of RC4.
However, it’s worth noting that there are other ciphers with similar naming conventions, such as RC2 and RC5, which were also developed by Ron Rivest. Each of these ciphers is distinct in its design and operation. RC2 is a block cipher, while RC4 is a stream cipher, and RC5 has a unique variable block size, key size, and number of encryption rounds. These ciphers are less frequently mentioned in general discussions about cryptography because they have been superseded by more advanced and secure algorithms. For instance, the Advanced Encryption Standard (AES) is now widely used and recommended for most applications due to its robust security and efficiency. The evolution of cryptographic algorithms is driven by the need for stronger security measures as computing power increases and new vulnerabilities are discovered in older algorithms.
ChaCha20
ChaCha20 is a stream cipher designed for high performance in software implementations. It’s known for its speed and security, particularly in encrypting data on platforms where cryptographic hardware support is unavailable. As a stream cipher, it encrypts plaintext one byte at a time, similar to RC4, but with enhanced security features and efficiency.
ChaCha20 was created by Daniel J. Bernstein, a well-known cryptographer, and first published in 2008. It was developed as an improvement on the earlier cipher Salsa20, also designed by Bernstein. ChaCha20 gained attention for its robustness and simplicity, making it a favorable choice in various cryptographic applications.
Number 20 (in ChaCha20) signifies the number of rounds of operations the algorithm performs on its internal state during encryption. Each round consists of complex mixing operations, totaling 20 rounds.
The algorithm operates using a unique approach that combines the best of both stream and block ciphers. The technical workings can be outlined as follows:
Step 1: Initial Setup; The Key, Nonce, and Counter
Let us imagine ChaCha20 as a lock.
To set it up, you need three things:
- Unique key: complex and private, 32 bytes long (256 bits). It is generated through a secure random number generation process, ensuring that the key is unpredictable and unique.
- Special one-time password (nonce): 12 bytes (96 bits) long, ensuring each encryption session is unique. The reason why it is a large number is to ensure the uniqueness of each encryption operation, greatly reducing the likelihood of any repetition across encryptions.
Similar to the secret key, is generated using a secure random number generation process. However, it doesn’t need to be kept secret, it is a public value and can be shared in clear text. It’s crucial that the nonce is never reused with the same key, as this can compromise security. - Counter: act as a stopwatch, starting at zero and going up each time you use the lock, ensuring every operation is distinct. Unlike both secret key and nonce, counter is not randomly generated; it’s a sequential number that starts at a specific value (often zero) and increments with each block of data encrypted using the same key and nonce.

In the context of ChaCha20, “block of data” refers to how the algorithm internally processes the data in fixed-size chunks (blocks) to generate the keystream. The ChaCha20 algorithm encrypts every byte chunk (8-bit) of the plaintext with another byte (8-bit) from the keystream, this is the reason why sometimes you hear the word “Block” in ChaCha20 even though it is a stream cipher algorithm.
Step 2: State Initialization; Setting the Combination
The lock has a combination (or state) mechanism setting inside of it which is a 512-bit state, you can think about it as a series of 512 dials, and each dial represents one bit.
Dial is not an official term in ChaCha20 algorithm, we just used it as an analogy to simplify the technical process operation.
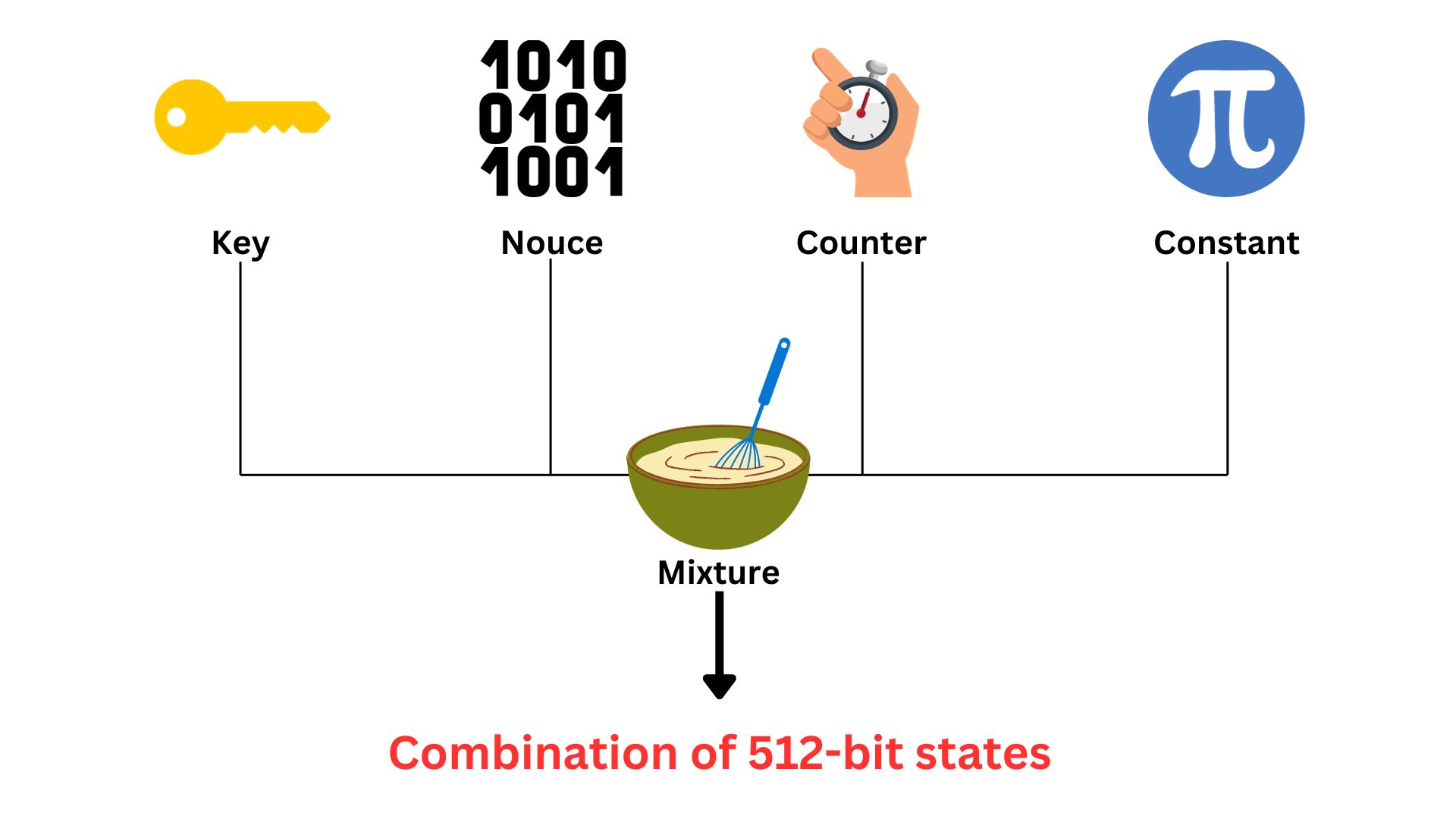
Let us have a simple example, we’ll use just 4-bit (4 dials) (as a mini state). Think of each dial as capable of being set to either 0 or 1, since a bit can only have these two values.
Setting Up Our Mini State (4-bit state):
- Dial 1 represents the first bit of our state.
- Dial 2 represents the second bit.
- Dial 3 represents the third bit.
- Dial 4 represents the fourth bit.
Let’s say our mini state starts like this:
- Dial 1 is set to 0.
- Dial 2 is set to 1.
- Dial 3 is set to 0.
- Dial 4 is set to 1.
So our starting state looks like 0101. Each dial (bit) contributes to this overall pattern.
In the actual ChaCha20 cipher, there are 512 such dials, creating a much more complex and larger pattern. The combination is formed from a complex mixture of three fixed numbers mentioned earlier; unique key, one-time password (nonce), counter, plus Constants. These constants refer to fixed, predefined values used in the initial state setup. They are in the format of a 32-bit series. These are standard numbers included for algorithmic consistency and to help differentiate ChaCha20’s operations from other processes. The combination (or the state) is the starting point for the encryption process. It will be used later to generate the keystream.
The principle is each bit (dial) plays a part in forming the initial state, which then undergoes various transformations during the encryption process. Each bit contributes to the overall complexity and uniqueness of the encryption mechanism.
Step 3: 20 Rounds of Operation
The combination (state) we talked about earlier has first to go through diffusion and confusion processes before the encryption starts. ChaCha20 performs 20 rounds of operations on the state. In each of the 20 rounds, ChaCha20 performs a series of transformations on this state. Each round consists of quarter-round operations that mix the input bits, providing diffusion and confusion, essential properties for secure encryption. These operations are based on basic arithmetic operations (addition, XOR, and left rotation), making them highly efficient in software.
This complex operation aims to change the bits’ positions and values, enhancing the security of the state. After all 20 rounds, this thoroughly mixed and transformed state is used to generate the keystream for encryption. These rounds ensure that the final keystream is highly unpredictable and secure, deriving from but significantly different from the initial combination.
If we continue on the 4-bit mini state (using it for easier understanding) we had before which is 0101 to illustrate the concept of the 20 rounds of operations in ChaCha20
Starting State (Mini State): 0101
Quarter-Round Operations:
There are multiple quarter-round operations, involving mixing of the bits. It’s called a quarter-round because each operation acts on a quarter (one-fourth) of the cipher’s state at a time. In ChaCha20, which has a 512-bit state, a quarter-round operation manipulates 128 bits (a quarter of 512 bits), hence the term quarter-round. Each round consists of four quarter-rounds, therefore, with 20 rounds in total, the cipher performs 80 quarter-round operations (20 rounds × 4 quarter-rounds per round). This approach enhances security through complexity comparing it if you are doing the 512-bit altogether, it allows for a more complex mixing of bits within smaller sections, increasing the cipher’s resistance to attacks.
For our mini state, let’s simplify this to one operation per round. We’ll use a basic operation like flipping the bits (just for illustration).
Round 1: Flip each bit.
- Starting State: 0101
- After Round 1: 1010 (each bit is flipped)
Round 2: Let’s say we rotate the bits to the left.
- Starting State: 1010
- After Round 2: 0101
Repeat for 20 Rounds: In actual ChaCha20 (state of 512), each round consists of more complex operations (addition, XOR, left rotation), but for our example, we’ll just alternate flipping and rotating.
When the final Round ends, after going through these operations 20 times, the state will have changed significantly from its original form.
This illustration is a vast simplification and doesn’t represent the actual complexity and security of ChaCha20’s operations. However, it gives a basic idea of how the state is transformed over multiple rounds, making the final state very different from the initial state.
One important factor we would like to highlight that is the four quarter-round operations in each round are not distinct types like XORing in one and rotating in another. Instead, each quarter-round operation involves a similar set of processes (like addition, XOR, and rotation) but acts on different sets of 128 bits within the 512-bit state.
Step 4: Keystream Generation
The 20 rounds we talked about will end generating the Keystream which is a 512-bit output block. This is like a secret code that’s unique every time you use the lock.

Step 5: Encryption and Locking the Message
To lock the message (plaintext), ChaCha20 uses this keystream. It does this by XORing the code with the message, byte by byte. Each byte of plaintext is XORed with a corresponding byte from the keystream. This XOR operation is bitwise, it compares each bit of the plaintext byte with the corresponding bit in the keystream byte. If the bits are different, the result is 1 (true); if the same, the result is 0 (false). If your message is longer, ChaCha20 just generates more of this keystream as needed. Each byte of your message gets its unique part of the keystream, making it securely locked.
Step 6: Incrementing the Counte, Keeping Each Use Unique
Every time you use ChaCha20 to lock a message, the counter increases by one. It ensures that the next time you encrypt something, even with the same key and nonce, the combination is different, resulting in a different ciphertext. This feature is crucial for stream ciphers, where ensuring uniqueness for each operation is key to maintaining security.
ChaCha20 Real Example
Let’s consider Alice wants to securely send a 100MB file to Bob using ChaCha20 encryption. Alice starts by generating a secret key, like choosing a unique, unbreakable password. This key is shared securely with Bob (typically through PKI and Diffie-Hallman key exchange protocols). She also creates a nonce, a one-time code like a disposable password, which can be shared openly.
Alice sets up her 512-bit state of ChaCha20. She carefully places the key, nonce, and a starting counter (like setting a timer to zero) into this state, along with fixed constants. The 512-bit state undergoes 20 rounds of operations, each round twisting and turning the bits in complex patterns. Each round consists of 80 quarter-round operations, meticulously manipulating 128 bits at a time, like a master locksmith crafting a unique key pattern. From this emerges a keystream, a unique sequence of bytes.
Alice’s file is broken into byte-sized pieces. Each byte of the file is then transformed, locked away by being combined (XORed) with the corresponding byte from the keystream. The result is a ciphertext, a securely locked version of her file.
As the process continues, Alice’s counter ticks up, ensuring that each subsequent chunk of data gets a fresh, unique part of the keystream, like changing the pattern of the magic ribbon for every new piece of the file. A keystream should not be used twice to encrypt the next byte of the plaintext, the algorithm should generate a new one including the effect of the counter.
With the same key, Bob can unlock the treasure using a reverse process, revealing the original file.
Today, ChaCha20 is considered highly reliable and secure, which has led to its widespread adoption in various cryptographic protocols. Its reliability stems from several factors:
- It has shown strong resistance to known cryptanalytic attacks. The design principles behind it, including the high number of rounds and the use of well-understood arithmetic operations, contribute to its robustness.
- It performs exceptionally well on a wide range of processors, especially those without specialized cryptographic hardware. This makes it a preferred choice in scenarios where hardware support for AES (Advanced Encryption Standard) is absent.
- ChaCha20, combined with Poly1305 for message authentication, has been adopted in important security protocols such as TLS (Transport Layer Security) and is used by major tech companies for encrypting web traffic. This combination is known as ChaCha20-Poly1305 and is recognized for its high-speed and security, making it a strong competitor to AES-based ciphers.
- The open and scrutinized nature of ChaCha20’s design contributes to its trustworthiness. Security experts have extensively analyzed it, and no significant weaknesses have been found.
Quiz Quiz
Data Encryption Standard (DES)
The Data Encryption Standard (DES) is a Block Cipher Symmetric Key encryption algorithm. Introduced in the 1970s by IBM, DES was one of the first widely accepted, publicly accessible encryption systems, setting a foundation for digital data security. Unlike modern algorithms that use large key sizes, DES is based on a smaller 56-bit key, encrypting data in 64-bit blocks. When DES was developed by IBM in the early 1970s, it was adopted as a federal standard by the United States National Bureau of Standards (now NIST) in 1977. Its development was influenced by work with the National Security Agency (NSA) to ensure its security for government and commercial use.
DES operates on a block cipher principle, encrypting and decrypting data in fixed-size blocks (64 bits in this case). The process involves several steps:
Key Size: 56-bit
Block Size: 64-bit
In cryptography, a “block” refers to a fixed-size group of bits processed as a single unit. It’s not exactly an “array” in the programming sense, but conceptually similar. A block is like a chunk of data that the algorithm works on, similar to an array holding a sequence of bits.
Step 1: Key Schedule Generation
DES takes the 56-bit key (generated through a secure random number generation process) and generates sixteen 48-bit keys through a process called the key schedule. DES performs 16 rounds of encryption on each plaintext message, and in each round, it uses a separate sub-key of 48-bit.
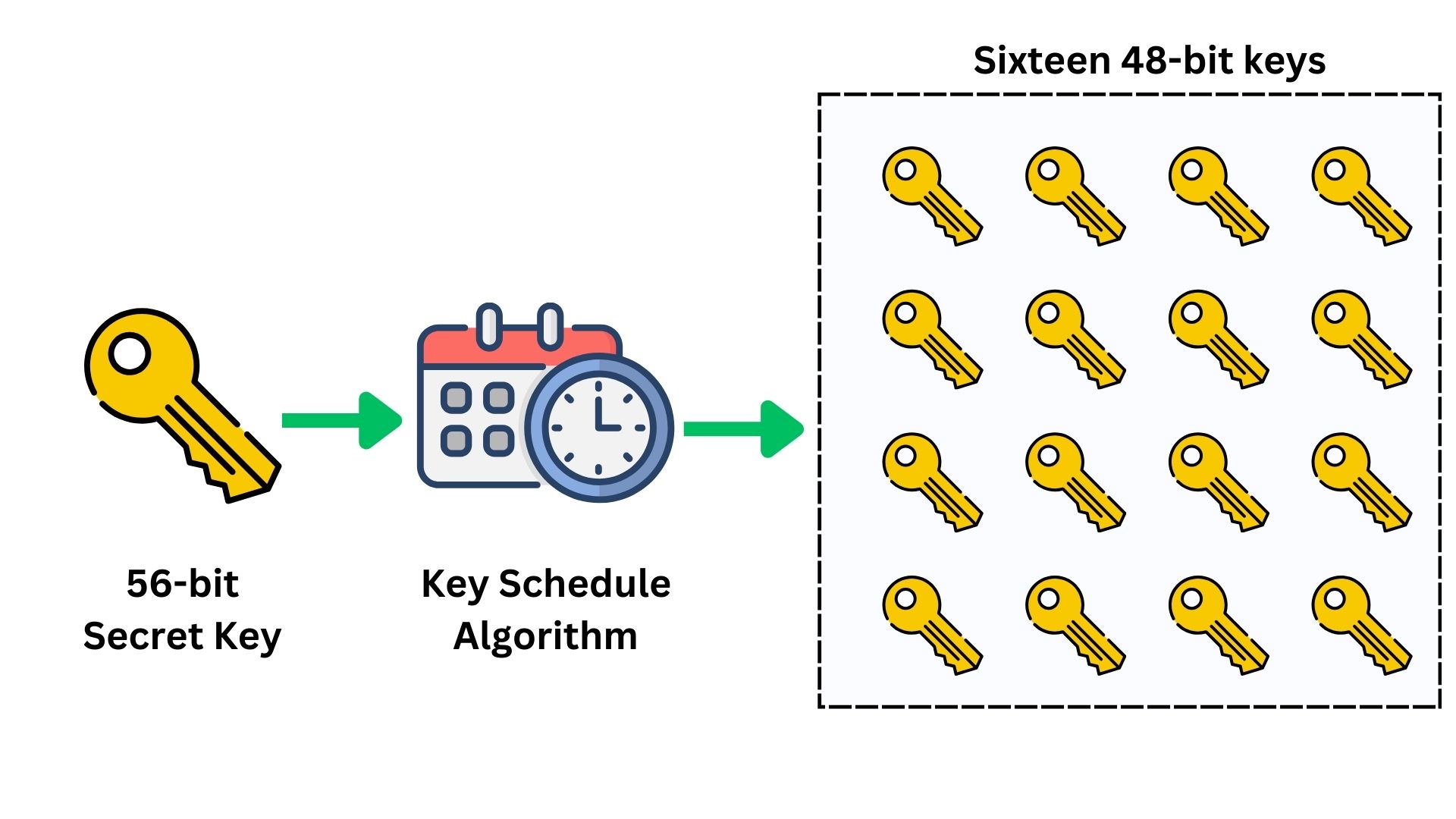
The key schedule algorithm of DES splits the 56-bit key into two halves (two of 28-bit). This is done for the generation of the 16 distinct sub-keys used in each encryption round as explained. This algorithm is responsible for the expansion, substitution, permutation, and mixing of the data with sub-keys. It ensures that each sub-key is unique and distinct.
Step 2: Initial Permutation (IP)
The 64-bit data block passes through an Initial Permutation (IP), rearranging the bits to break up patterns.
Step 3: 16 Rounds of Processing
The core of DES involves 16 rounds of processing the data, encryption of plaintext data. Each round includes:
Expansion: The original plaintext data has to be formed first in blocks of 64-bit size. Then each block will be divided into half data blocks (32 bits each). After that, these 32-bit blocks are expanded to 48 bits using a predefined expansion table. This helps in the mixing of bits.
Key Mixing: The expanded block (48-bit) is mixed with a sub-key (48-bit) using the XOR operation.
Substitution: The result is then passed through a series of S-boxes (substitution boxes). Each S-box is a predefined table that replaces 6-bit input with a 4-bit output, introducing non-linearity and complexity.
Non-linearity in cryptography refers to a property where the relationship between the input and output is not straightforward or predictable, making it difficult to deduce the input from the output using linear methods.
An S-box (Substitution box) in cryptography is a fundamental component used to perform substitution.
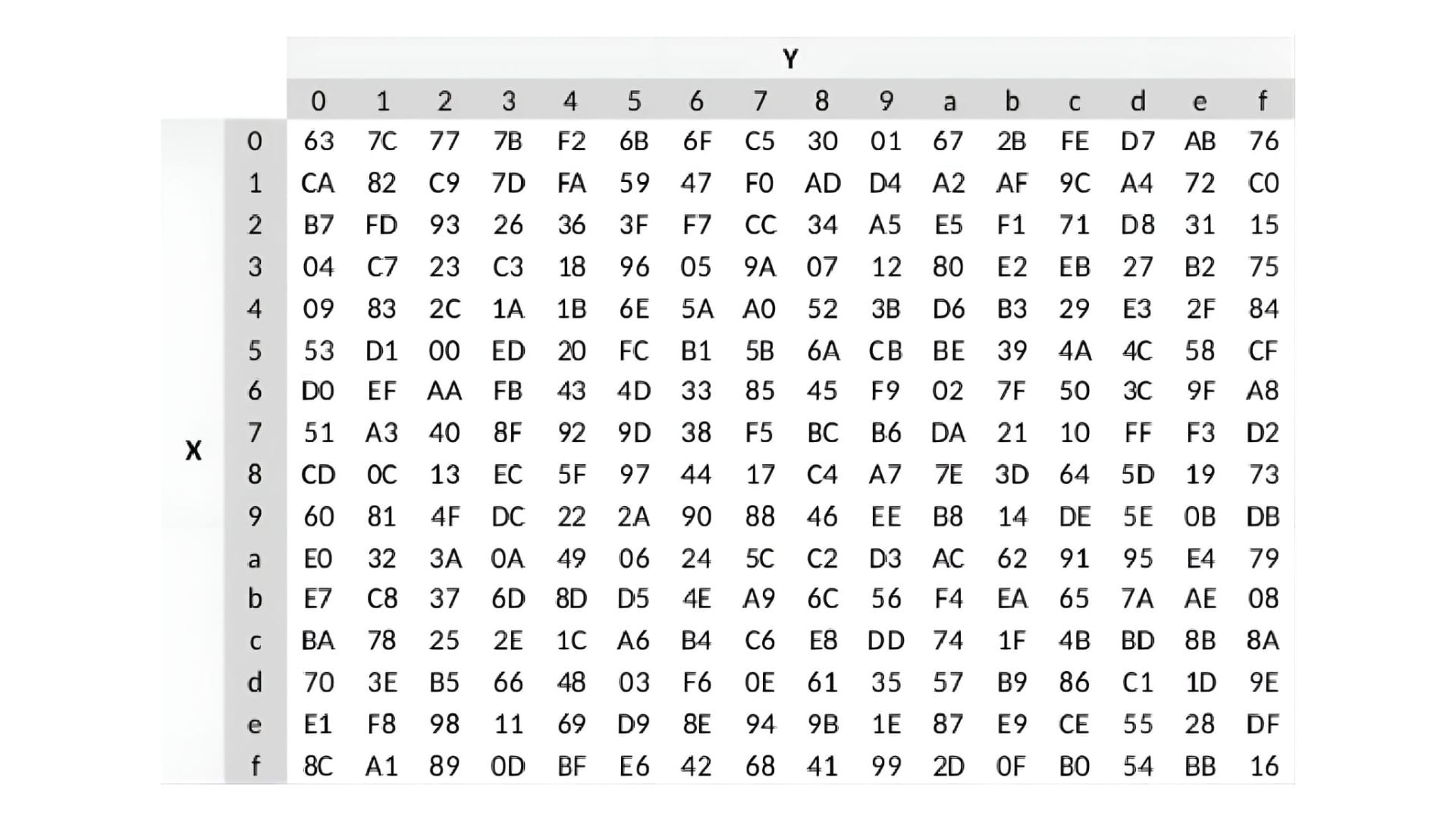
In DES, it transforms a 6-bit input into a 4-bit output based on a predefined set of rules or a lookup table. This process introduces complexity and non-linearity, crucial for secure encryption.
Each S-box uses a 6-bit input, where the outer two bits determine the row (Y-axis) and the middle four bits select the column (X-axis) in a 4×16 table. These axes, labeled 0 to F in hexadecimal, guide the lookup process to find the corresponding 4-bit output.
Let us have it in an example, imagine you have a 6-bit input; 110101. To use the S-Box, we take the first and last bits (11, which is binary for 3 in decimal) to select the row, and the middle four bits (1010, which is binary for 10 in decimal) to select the column.
The first and last bits are 11. In binary, 11 is 3 in decimal, so we select row 3.
The middle four bits are 1010. In binary, 1010 is 10 in decimal, so we select column a.
Now, we find the intersection of row 3 and column a in the table, which gives us the hexadecimal value of 80. In binary, 80 is 10000000. Since we only need a 4-bit output, we take the last four bits: 0000.
So, the 6-bit input 110101 has been transformed through the S-Box to a 4-bit output 0000. This process introduces non-linearity, making the encryption more complex and secure.
During decryption, the recipient uses the same S-boxes in reverse as part of the DES decryption process. They apply the inverse operations of the final permutation, the rounds (in reverse order), and the initial permutation. However, S-boxes don’t directly reverse; instead, they’re part of the larger DES algorithm that, when reversed, allows the original plaintext to be accurately reconstructed from the ciphertext. The recipient doesn’t reverse the S-box output itself; they use the entire decryption process, which takes the transformed output, applies the inverse of the entire encryption process including the 16 rounds with the sub-keys, and arrives back at the original 6-bit input. The S-boxes are a step in the encryption that adds complexity, but the overall DES algorithm is designed so that when the correct key is used, the original plaintext emerges at the end of decryption.
Permutation: The output of the S-boxes goes through a permutation designed to spread the bits across the block, preparing it for the next round.
The same process that we explained; Expansion, Key Mixing, Substitution, and Permutation go 16 times on each plaintext message.
Step 4: Final Permutation
After the 16 rounds, a final permutation (inverse of the initial permutation) is applied, producing the ciphertext.
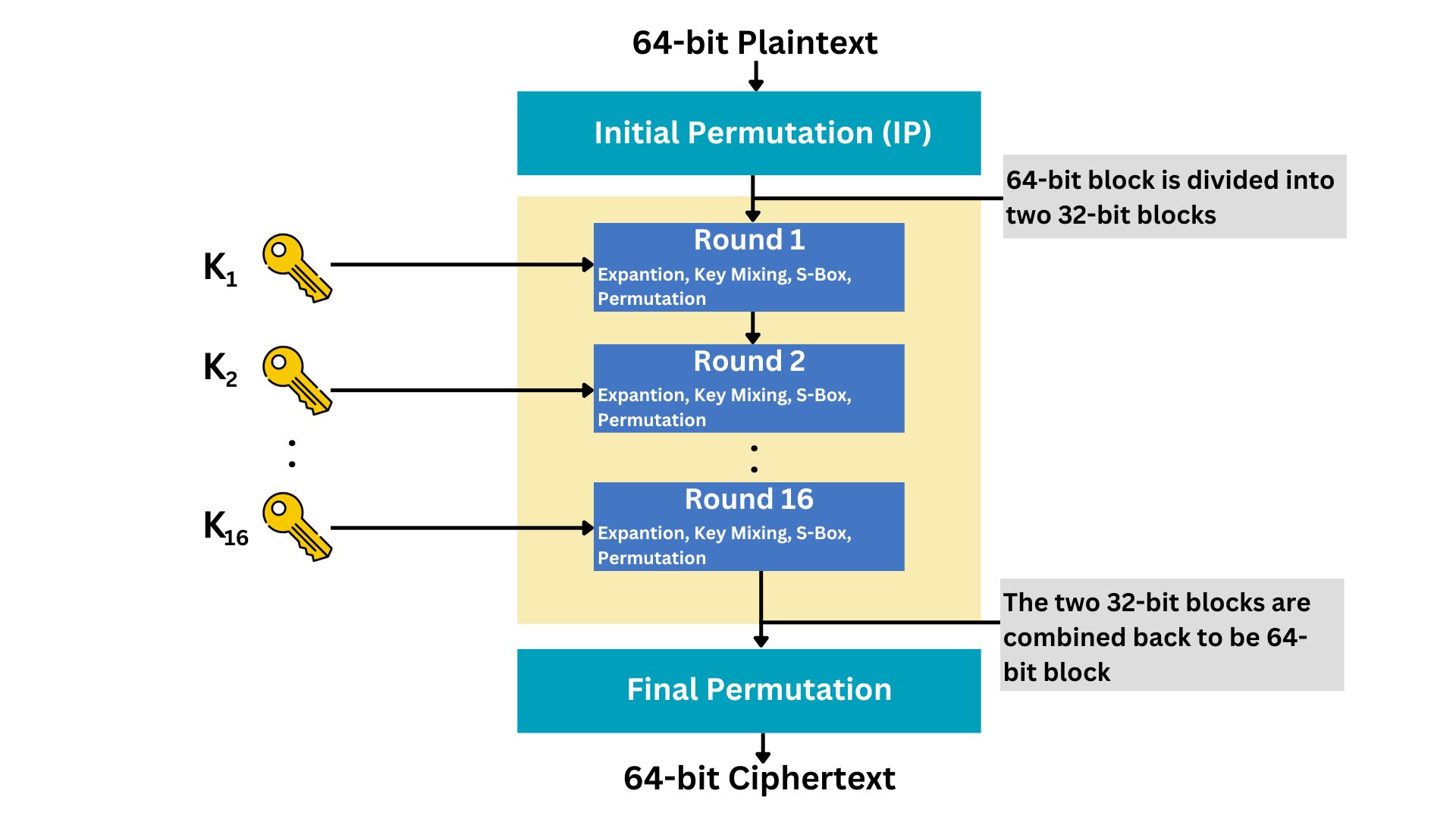
Note that if you have 100 plaintext messages, they will be encrypted using the same 16 sets of sub-keys, unless you change the initial secret key.
Decryption in DES uses the same steps but applies the sub-keys in reverse order.
Today, DES is considered insecure for most applications due to its short key length (56 bits). With advancements in computing power, especially with the advent of large-scale parallel processing and techniques like brute-force attacks, DES can be relatively easily broken. For example, in the late 1990s, specialized machines were built that could break a DES encryption in a matter of days or even hours.
However, DES’s influence remains significant in the field of cryptography. Its design principles, especially the concept of S-boxes and the general structure of a block cipher, have influenced subsequent encryption algorithms. DES also paved the way for more advanced iterations like Triple DES (3DES), which was designed to extend the viability of DES by running the encryption process multiple times with different keys.
Double DES
Double DES, or 2DES, is an extension of the Data Encryption Standard (DES) encryption algorithm that was designed to provide a deeper level of security through a method called double encryption. Essentially, it involves running the standard DES algorithm twice, with two different keys.
Double DES emerged as a natural progression from the original DES, which by the late 1970s and early 1980s, was beginning to be considered vulnerable to brute-force attacks due to its relatively short key length. The exact date of 2DES’s inception isn’t as well-documented as that of DES, but it was recognized during the 1980s as cryptographers sought to enhance the DES algorithm against increasing computational power.
It is built upon the original DES algorithm. Instead of encrypting data once, 2DES applies the DES encryption process twice in succession.
Key Size: 56-bit (two distinct keys are used)
Block Size: 64-bit
- First Encryption Pass: The plaintext data is encrypted with the first 56-bit key using the DES algorithm, resulting in ciphertext 1.
- Second Encryption Pass: The resulting ciphertext 1 from the first encryption is then encrypted again using a second, distinct 56-bit key, resulting in ciphertext 2 (the final one).
Note that 2DES runs through 32 rounds of the DES algorithm, 16 rounds for the first key and another 16 rounds for the second key. 2DES from high-level looks like this:

In every encryption process which consists of 16 rounds as we discussed previously in DES, the same principles apply to 2DES except it happens twice, each with a different key.
However, 2DES does not significantly improve security because it is vulnerable to a type of attack called a meet-in-the-middle attack. This attack effectively reduces the security provided by the two separate keys to be not much more than that of a single DES encryption.
For a meet-in-the-middle attack to work against Double DES, the attacker needs at least one pair of plaintext and its corresponding ciphertext. The attack works as:
- The attacker takes a known 64-bit plaintext and its corresponding 64-bit ciphertext.
- The attacker encrypts the known plaintext with every possible key (2^56 possibilities for DES) and stores these results.
Note that, when the attacker tries to encrypt the known plaintext, they don’t use the 48-bit sub-keys directly. Instead, they use the full 56-bit key to run the entire DES encryption process, which internally generates and applies these 16 sub-keys in its 16 rounds of encryption. Each possible 56-bit key leads to a different set of 16 48-bit sub-keys and thus a different result after 16 rounds of encryption.
The 16 sub-keys are predictable if you have the original 56-bit secret key. - Separately, the attacker also decrypts the known ciphertext with every possible key (another 2^56 possibilities).
- The attacker looks for a match between the results of the forward encryption and backward decryption. Forward encryption refers to encrypting plaintext with Key 1 in Double DES, and backward decryption means decrypting the final ciphertext back to this first ciphertext using Key 2. If a match happens, it means these are the right keys used.
- The attacker then tests these key pairs to verify if they correctly encrypt and decrypt other plaintexts and ciphertexts.
The following image illustrates the meet-in-the-middle attack process:
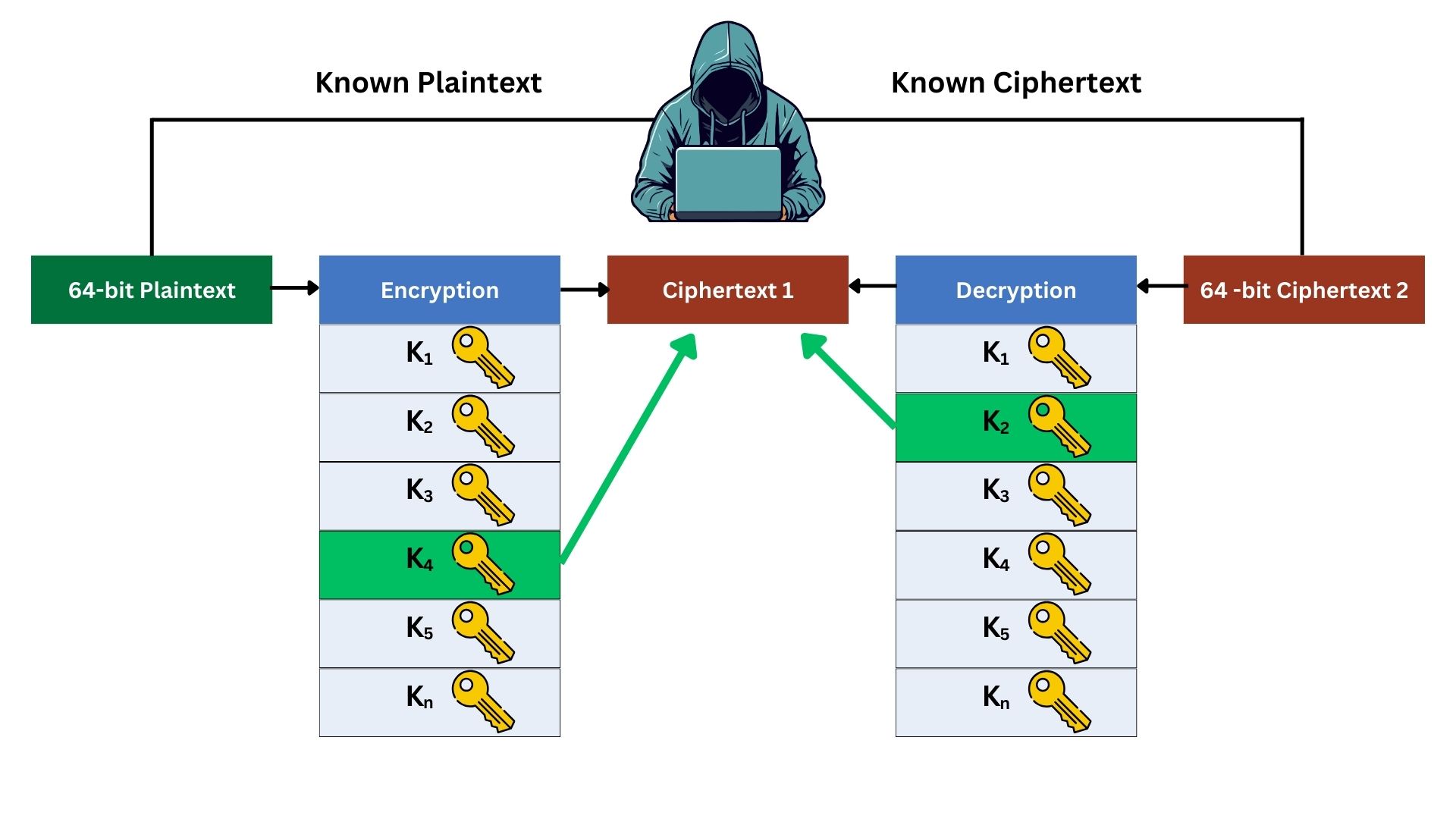
In this simplified example, the attacker brute-forced the original known plaintext, encrypting it with all the possible keys, and he kept the result record. On the other hand, he decrypted the known ciphertext with all possible keys. Then he noticed that Key 4 from the left side brute-force record and Key 2 from the right side brute-force record resulted in the same ciphertext, which means they are the keys used in this 2DES operation.
If a computer cracks DES in 4 hours, theoretically, it might crack 2DES in roughly 8 hours, which is no big security difference.
The meet-in-the-middle attack requires significant storage. The attacker needs to store the results of encrypting the plaintext with all possible keys and the results of decrypting the ciphertext with all possible keys. This storage requirement, which involves billions of possible keys and their corresponding results, can be substantial.
2DES is not considered secure and is not implemented in modern security protocols. It is not approved by standards organizations for protecting sensitive data. After vulnerabilities were discovered in Double DES, Triple DES (3DES) was introduced. 2DES is not used in real-world applications.
Triple DES
Triple DES (3DES) is an enhancement of the original Data Encryption Standard (DES) algorithm, designed to provide stronger encryption by using multiple rounds of DES. It was developed to counteract the vulnerabilities of DES, especially its susceptibility to brute-force attacks due to the relatively short 56-bit key length. 3DES employs a sequence of three DES operations with two or three different keys, significantly increasing the security of the encryption.
This version of DES came into use in the late 1990s as a practical and straightforward way to extend the lifespan of the DES algorithm. It was formally adopted as a standard by the National Institute of Standards and Technology (NIST) in 1999.
3DES was developed primarily to address the vulnerabilities of DES, not specifically those of 2DES. By employing multiple DES encryption operations (three) with different keys, 3DES significantly enhanced security over the original DES, countering its key length and brute-force vulnerabilities, rather than being a direct response to 2DES’s shortcomings. While 2DES does use more than one key and multiple operations, it remains vulnerable because the meet-in-the-middle attack effectively neutralizes the advantage of using two keys. 3DES, however, uses a third encryption operation, significantly increasing security and mitigating the meet-in-the-middle vulnerability present in 2DES.
In a nutshell, 3DES makes brute-force attacks much more difficult. However, the core algorithm principles remain fundamentally the same as DES, but the additional layers of encryption with different keys significantly increase the complexity and security.
The industry did not immediately move to a different encryption algorithm because DES was already widely implemented in various hardware and software systems. Transitioning to a completely different algorithm would have required significant changes and investments. 3DES offered a more convenient and cost-effective solution by enhancing the existing DES infrastructure, thereby providing improved security without the need for extensive system overhauls.
The following illustrates the process of how the 3DES algorithm works:
Key Size: 112 bits (using two distinct keys ‘2x 56-bit’) or 168 bits (using three distinct keys ‘3x 56-bit’)
Block Size: 64-bit
Step 1: Keying Options
3DES uses either three keys (keying option 1) or two keys (keying option 2). These keying options in 3DES refer to the different ways the keys are used in the encryption process.
In Keying Option 1, three distinct 56-bit keys are used, making the effective key size 168 bits. This option involves three separate DES operations, each with a different key.

In Keying Option 2, two 56-bit keys are used, making the effective key size 112 bits. Here, the first and third DES operations use the same key, while the second operation uses a different key, totaling three DES operations but with only two unique keys.
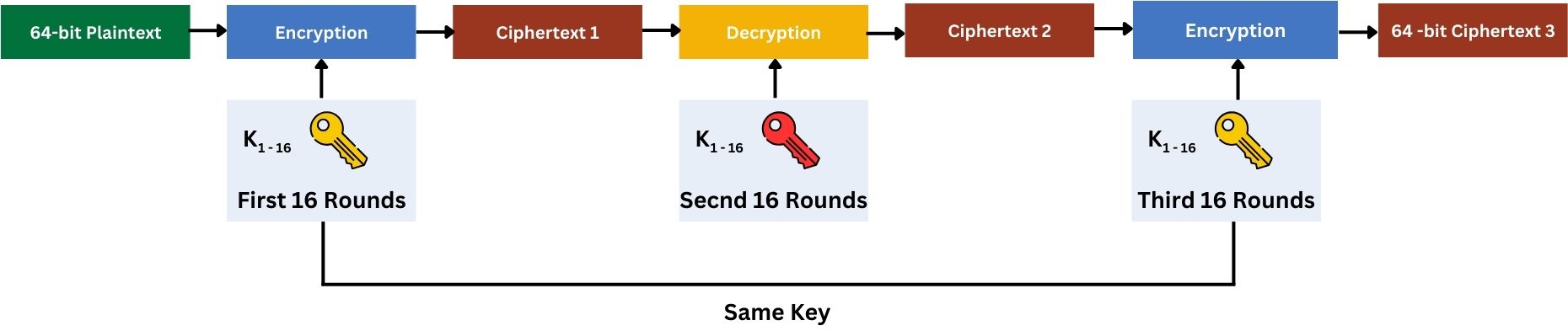
These options exist to provide a balance between security and key management. Option 1 offers more security due to three distinct keys, while Option 2 simplifies key management with only two keys yet still enhances security compared to the original DES.
Step 2: Initial Data Preparation
Like DES, 3DES works on 64-bit blocks of data. The data to be encrypted is prepared in blocks of this size.
Step 3: First DES Operation (Encryption)
The first step in 3DES is to encrypt the data block using the DES algorithm with the first key (K1). This step is similar to the standard DES encryption process, involving initial permutation, 16 rounds of processing (expansion, substitution, permutation, and mixing with a sub-key), and a final permutation.
Step 4: Second DES Operation (Decryption)
The output from the first DES encryption is then processed using DES decryption with the second key (K2). This might seem counterintuitive, but using a decryption operation in the middle step adds to the complexity and security of the overall encryption process.
Step 5: Third DES Operation (Encryption)
The result of the second step is then encrypted again using the DES algorithm, this time with the third key (K3), which may be the same as K1 in the two-key variant.
Step 6: Final Output
The output of the third DES operation is the final ciphertext.
To decrypt, the process is reversed, first decrypt with K3, then encrypt with K2, and finally decrypt with K1.
The use of multiple keys and the encryption-decryption-encryption sequence make 3DES much more secure than single DES. However, it also makes 3DES slower compared to DES, as it essentially runs the DES algorithm three times.
3DES has been a reliable and widely adopted encryption standard, especially in financial services and other industries where data security is crucial. However, like DES, 3DES has begun to show its age. Especially when the CVE-2016-2183 vulnerability was discovered, also known as the “SWEET32” vulnerability, is associated with 3DES. It highlights a weakness in 3DES used in TLS and other cryptographic protocols. This vulnerability arises from the small block size (64 bits) of 3DES, which makes it susceptible to collision attacks after processing many gigabytes of data. This can potentially allow attackers to decrypt HTTPS traffic, exposing sensitive data. Consequently, the use of 3DES has been discouraged in secure communications.
3DES was considered a secure and trusted algorithm until the mid-2010s. Around 2015-2016, with the increased awareness of vulnerabilities like SWEET32 and advancements in computing power, the perception of its security diminished, leading to recommendations for transitioning to more secure algorithms like AES.
Advanced Encryption Standard (AES)
The Advanced Encryption Standard (AES) is a symmetric block cipher encryption algorithm widely used across the globe to secure data. It was developed to replace older encryption standards like DES and 3DES, offering enhanced security, efficiency, and flexibility. Unlike its predecessors, AES operates on block sizes of 128 bits and offers key sizes of 128, 192, or 256 bits. This provides a significantly higher level of security compared to DES’s 56-bit or 3DES’s 112/168-bit keys. AES employs a series of operations; substitutions, permutations, and mixing of data across multiple rounds of processing:
10 rounds for 128-bit keys
12 rounds for 192-bit keys
14 rounds for 256-bit keys
Each round involves a complex transformation of the block, ensuring robust encryption. The design of AES makes it resistant to all known practical cryptographic attacks, making it a standard for secure data encryption.
AES was released in 2001 by the U.S. National Institute of Standards and Technology (NIST) after a rigorous selection process. It was initially developed by two Belgian cryptographers, Vincent Rijmen and Joan Daemen. The selection process involved global cryptanalysis efforts from various experts to ensure its robustness. AES was chosen for its combination of security, performance, efficiency, simplicity, and flexibility. It was adopted as a federal standard by the U.S. government and has become one of the most popular encryption algorithms used worldwide.
The migration from 3DES to AES was driven primarily by the need for stronger security and greater efficiency. While 3DES was more secure than DES, it was still vulnerable to certain attacks and its smaller block size (64 bits) became inadequate against modern cryptanalytic techniques. Furthermore, 3DES’s triple encryption process made it significantly slower than AES. AES, with its larger block and key sizes, offers enhanced security against brute-force attacks and sophisticated cryptanalytic methods. Additionally, AES’s efficient algorithm design allows for faster processing speeds, making it more suitable for modern computing environments, including hardware with limited resources. This combination of high security and performance efficiency made AES the preferred choice for replacing 3DES in various applications, including government and financial communications.
AES is a complex encryption algorithm, yet its fundamental principles can be explained in a clear and approachable manner. We’ll break down its process into major steps:
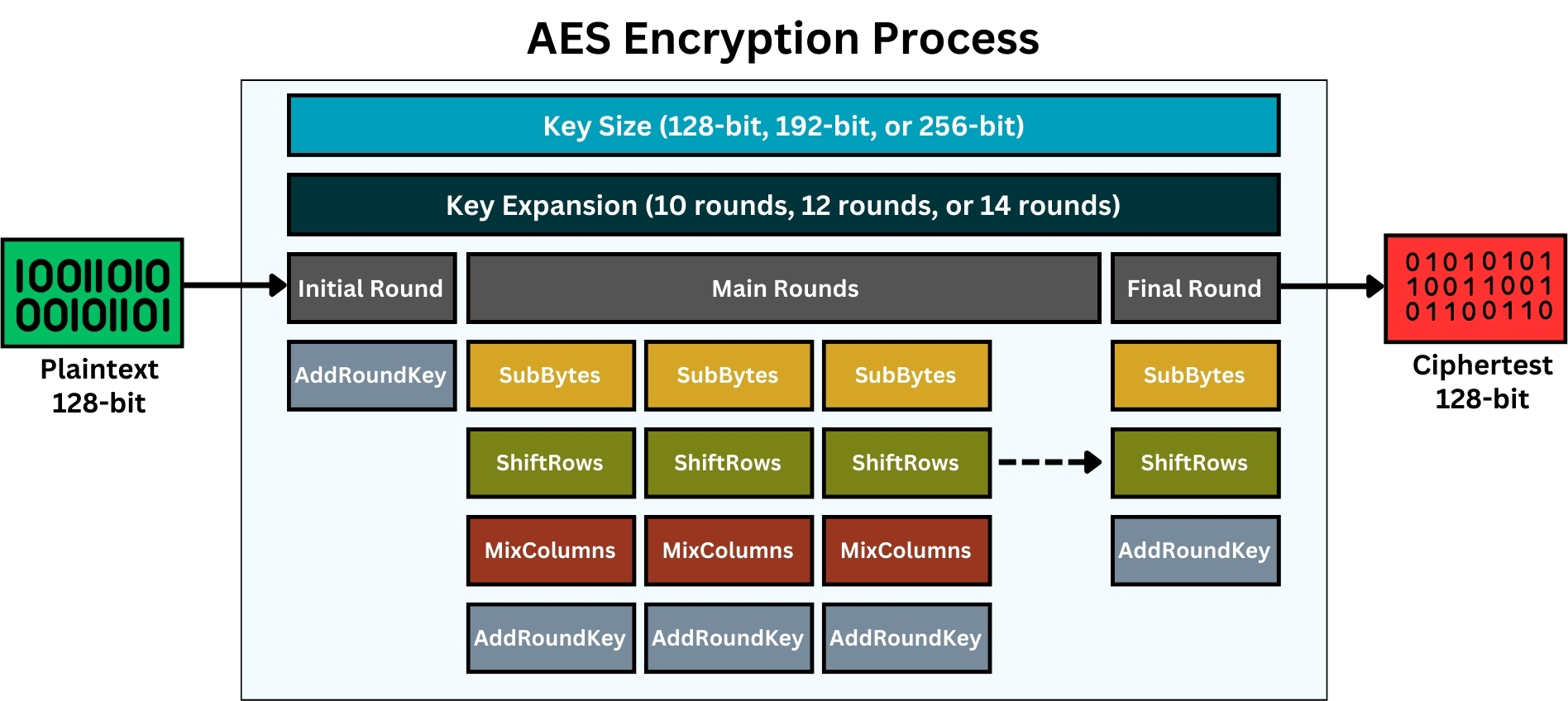
Step 1: Overview and Key Sizes
As we stated before, AES is a symmetric block cipher, meaning the same key is used for both encryption and decryption. It works on fixed data blocks of 128 bits and offers three key sizes; 128, 192, or 256 bits.
Depending on the key size, the number of encryption rounds differs; 10 rounds for 128-bit keys, 12 for 192-bit keys, and 14 for 256-bit keys.
Step 2: Initial Key Expansion
For each encryption round, a unique sub-key is derived from the main secret key, equal to the number of rounds. So, for a 128-bit key with 10 rounds, 10 sub-keys are generated; for a 192-bit key with 12 rounds, 12 sub-keys; and for a 256-bit key with 14 rounds, 14 sub-keys are created. These sub-keys are used in each round’s AddRoundKey step.
Each of the sub-keys generated in AES, regardless of the original key size, is exactly 128 bits to match the 128-bit block size. This is done through a series of operations including substitutions and permutations, generating a unique key for each round of the process.
Similar to the previous algorithms, the sub-keys in AES are predictable in the sense that if two parties know the initial key, they will both derive the exact same set of round keys. The key expansion algorithm in AES ensures consistent and replicable generation of round keys from the initial key.
Step 3: Initial Round
The initial round involves only the AddRoundKey step. This step requires mixing the data block with the first round key. This is done by a simple bitwise XOR operation between the data and the key.
The other steps like SubBytes, ShiftRows, and MixColumns are not used in the initial round. These steps begin from the first main round of AES and are repeated in each subsequent main round, up to the round before the final one.
The objective of this initial round is to integrate the first sub-key with the plaintext data without deeper and more complex operations found in later rounds, establishing an initial layer of security.
Step 4: Main Rounds
For each main round, four operations are performed:
- SubBytes: A non-linear substitution step where each byte is replaced with another according to a fixed table (S-Box).
S-Box is a fixed, predefined table, similar to the one used in DES. This table does not change and is the same for every AES encryption and decryption process.
- ShiftRows: A transposition step where each row of the block is shifted cyclically a certain number of times. The top row is not shifted, the second row is shifted one to the left, the third row two times, and the fourth row three times.
The concept of “rows” and “columns” in the AES block is a way to visualize the data for the purpose of explanation. In AES, the 128-bit block is often conceptualized as a 4×4 grid (or matrix) of bytes for ease of understanding the operations. Each cell includes 1 byte (8-bit), since there are 4×4 cells, this means 16 cells, resulting in a 128-bit block.
Remember, while a cryptographic block is not an array in the programming sense, this representation helps in comprehending steps like “ShiftRows” where data is manipulated in a structured, array-like format.
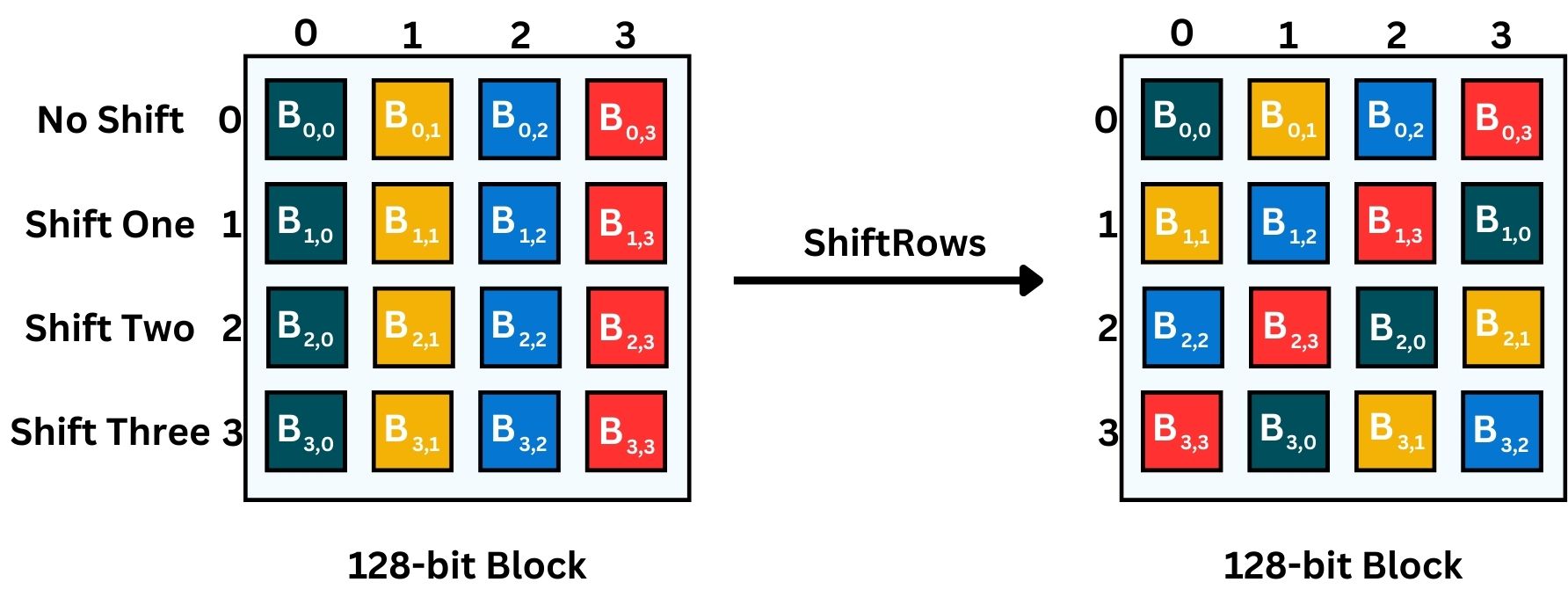
In the above image, we choose the letter B, indicating Byte.
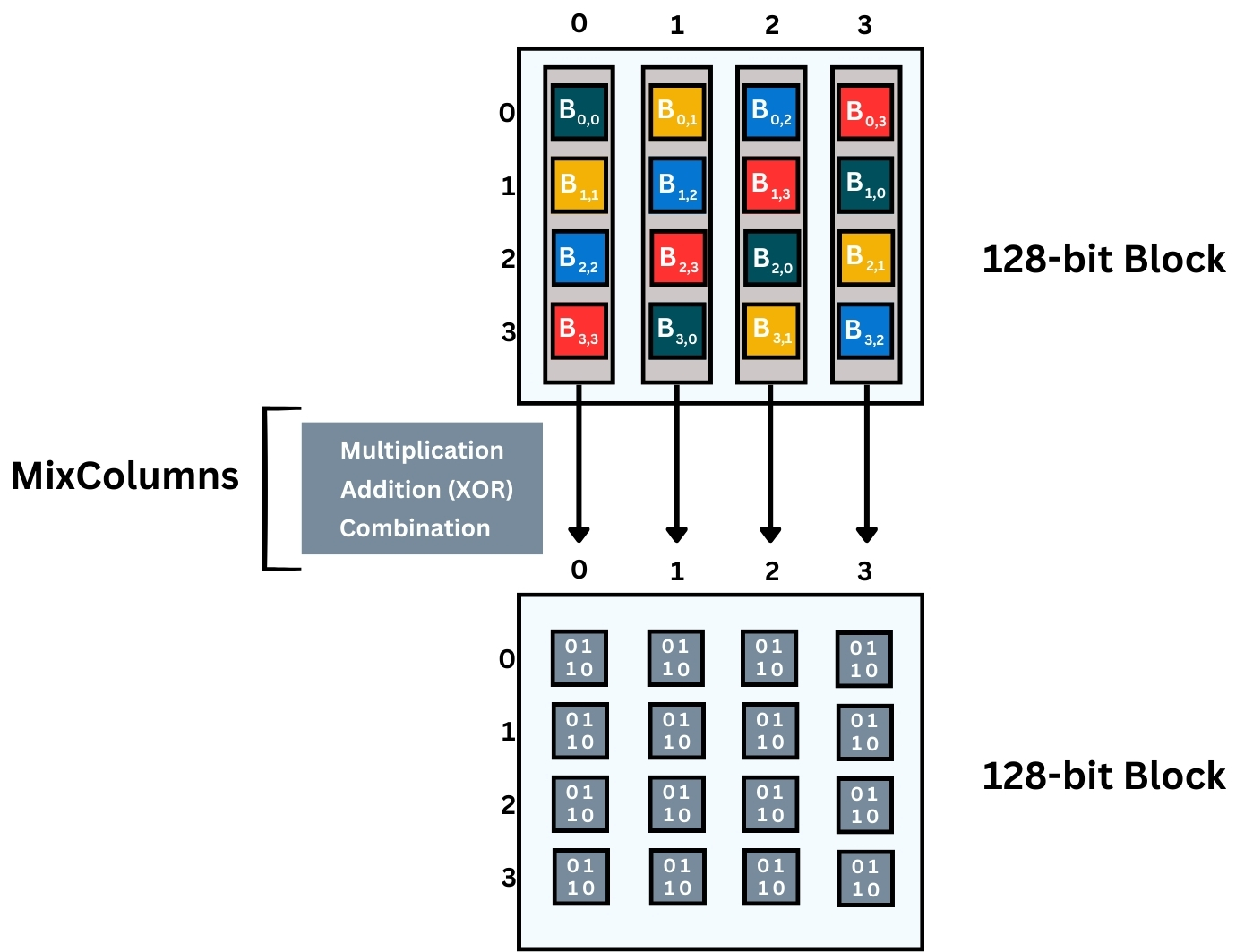
- MixColumns: This process follows the outcome of the ShiftRows process. MixColumns function ensures that changes to a single byte of the input affect multiple bytes of the output, contributing to the diffusion property.
It is a mixing operation that operates on each column individually. Each column is transformed using a fixed mathematical function, which helps in diffusing the data across the column.
MixColumns involves a fixed polynomial multiplication in the Galois Field (2^8), which can be complex to visualize in detail. But the key idea is that each column’s bytes are mixed and affect each other, resulting in entirely new columns. Each byte in the output columns is a combination of all four bytes in the input column, transformed by the MixColumns operation. This is a crucial step for ensuring the diffusion property in AES, where changes to one byte affect all bytes in the block. Here’s what happens in more detail:
A finite field is a mathematical construct where a set of numbers is limited, and all arithmetic operations within the set result in a number that is also within the set. It is like a clock face representing a finite field of 12 hours; adding 4 hours to 10 o’clock gives you 2 o’clock, not 14 o’clock.
Galois Field (GF) and finite field refer to the same concept. A Galois Field, named after mathematician Évariste Galois is a type of finite field with a finite number of elements that is (2^8). It is a mathematical system where a limited set of numbers can be added, subtracted, multiplied, and divided (excluding division by zero), resulting in a new number within the same set. In AES, the finite field GF(2^8) means all operations are performed on bytes (8 bits long) and always produce a byte as a result, ensuring consistency within the encryption process.
- Multiplication
Each byte in a column is multiplied by a fixed set of values from a predefined matrix. The matrix contains the constants {02}, {03}, {01}, and {01}, which are used for the multiplication. In AES, this multiplication isn’t standard arithmetic multiplication; it’s done in the context of a finite field, which means it follows special rules to ensure the results still fit within a byte. These constants are carefully chosen by the creators of the AES algorithm, Vincent Rijmen and Joan Daemen to ensure proper diffusion during the transformation. They selected these constants based on their cryptographic properties to ensure the security and efficiency of the algorithm. These constants are fixed and integral to the AES standard.
- Addition (XOR)
After the multiplication, the results are added together using the XOR operation. This isn’t standard addition but rather bitwise addition without carry, which in the context of finite fields, ensures non-linearity and maintains the byte size.
- Combination
The four bytes in each column are combined through these operations, and each operation affects the outcome of the others. The result is that the input bytes are thoroughly mixed to produce the new bytes of the column.
- AddRoundKey: Each byte of the state is combined with the round key using bitwise XOR.
Step 5: Final Round
In the final round, the MixColumns step is omitted. Only the SubBytes, ShiftRows, and AddRoundKey steps are performed. This ensures that the process is reversible for decryption.
Omitting MixColumns in the final round of AES is a design choice to simplify the decryption process.
AES decryption is not just the encryption process run backward. Each step has an inverse operation, and decryption involves applying these inverses in reverse order.
InvShiftRows, InvSubBytes, AddRoundKey, and InvMixColumns are used for each round in reverse order. The AddRoundKey step remains the same as in encryption but uses the round keys in reverse order.
The strength of the AES algorithm lies in its combination of substitution (SubBytes) and transposition (ShiftRows and MixColumns), complemented by the key addition (AddRoundKey), providing robust security. Its S-box, used in SubBytes, is resilient to linear and differential cryptanalysis. Additionally, the MixColumns function ensures that alterations to a single byte influence multiple bytes of the output, enhancing the diffusion property critical for secure encryption.
AES is designed to be efficient both in software and hardware implementations. It’s well-suited for a wide range of devices, from high-end servers to small embedded systems. The algorithm’s structure allows for parallel processing, making it very effective and fast on modern processors.
In conclusion, the AES algorithm is a masterpiece of cryptographic design, balancing security, efficiency, and flexibility. Its robustness against various types of attacks, combined with its performance characteristics, has made it the preferred choice for encrypting data in numerous applications worldwide. The step-by-step process of AES, from initial key expansion to the detailed operations of each round, showcases a level of cryptographic sophistication that ensures the confidentiality and integrity of data in the digital age.
Algorithms Comparision
The table below summarizes the cryptographic algorithms we’ve covered in this lesson, providing a quick comparison and overview of their key characteristics, performance, and current relevance in the field of cryptography.
| Criteria | RC4 | ChaCha20 | DES | 2DES | 3DES | AES |
|---|---|---|---|---|---|---|
| Origin | Ron Rivest, RSA | Daniel J. Bernstein | IBM (influenced by NSA) | Extension of DES | Extension of DES | Vincent Rijmen, Joan Daemen |
| Year of Introduction | 1987 | 2008 | 1977 | 1980s | Late 1990s | 2001 |
| Algorithm Type | Stream Cipher | Stream Cipher | Block Cipher | Block Cipher | Block Cipher | Block Cipher |
| Key Size (bits) | Variable, typically 40-2048 | 256 | 56 | 112 | 112/168 | 128/192/256 |
| Rounds | N/A | 20 | 16 | 32 (16 x 2) | 48 (16 x 3) | 10/12/14 |
| Block Size (bits) | N/A | N/A | 64 | 64 | 64 | 128 |
| Security Level | Weak (deprecated) | Strong | Weak (deprecated) | Weak (vulnerable to meet-in-the-middle) | Moderate (being phased out) | Very Strong |
| Speed/Performance | Fast | Very Fast | Slow | Slower than DES | Slower than DES | Fast |
| Design Goals | Simplicity, Speed | Security, Performance | Security (then) | Increased Security over DES | Increased Security over DES | Security, Efficiency, Versatility |
| Encryption Mode | N/A | N/A | ECB, CBC, others | Similar to DES | Similar to DES | ECB, CBC, GCM, others |
| Common Usage/Applications | Historically in SSL, wireless security | Web encryption, VPNs | Historical, banking | Not used | Banking, Government | Widespread in all domains |
| Known Attacks/Vulnerabilities | Numerous, including key recovery attacks | Relatively few known vulnerabilities | Differential, Linear Cryptanalysis | Meet-in-the-middle attack | Meet-in-the-middle, Related-key attacks | Side-channel attacks, but robust against cryptanalysis |
| Suitability for Hardware/Software | Better in Software | Excellent in both | Better in Hardware | Similar to DES | Similar to DES | Excellent in both |
| Standardization | No formal standard | Not formally standardized, widely adopted | ANSI, NIST | No standard | NIST | NIST, FIPS |
| License Requirements | Patent expired | Open Source | Initially IBM, now public domain | N/A | N/A | Open standard |
Quick Quiz
Summary
In this lesson, we’ve explored a range of Symmetric Encryption Algorithms, focusing on those most prominently used both in the past and present. While our coverage has been comprehensive, it’s important to note that the field of symmetric encryption is vast, with numerous other algorithms also playing significant roles in the evolution of data security. Our selection aimed to provide a broad understanding of the landscape, illustrating the progression and advancements in encryption technology over time.
One of the primary objectives of this lesson was to research into the factors that contribute to the strength of an encryption algorithm. We discussed the importance of key generation and key size, which are critical in determining an algorithm’s resilience against brute-force attacks. We also examined algorithm vulnerabilities, the concept and role of the keystream, and the significance of encryption rounds. The concepts of confusion and diffusion were highlighted as essential in the transformation of plaintext into ciphertext, underscoring how these cryptographic principles enhance security. Understanding these elements is crucial for appreciating what makes an encryption algorithm robust and effective in protecting data.
To conclude, we brought together our learning in a comprehensive comparison of the algorithms we covered. This comparative analysis not only showcased the unique attributes and historical significance of each algorithm but also provided a clear perspective on their relative strengths and weaknesses. As we wrap up, it’s clear that the field of symmetric encryption is dynamic and continually evolving, with each algorithm building upon the lessons learned from its predecessors to offer stronger, more efficient ways to secure our digital world.
Homework
- Investigate the expansion table used in the DES algorithm. Explain its purpose and how it contributes to the security of DES.
- For each Block Cipher Algorithm (DES, 2DES, 3DES, AES) discussed, research the different Modes of Operation (e.g., ECB, CBC, GCM). Analyze which mode best enhances the security of each algorithm and why.
- Conduct an in-depth study on the vulnerability CVE-2016-2183, often associated with 3DES. Discuss its implications and how it affects the security of data encrypted with 3DES.
- Research other popular symmetric encryption algorithms, either stream or block ciphers, that were not covered in this lesson. Provide an overview of their key features and current usage.
- Write a short essay on whether you prefer publicly disclosed encryption algorithms (open standards) or private algorithms. Include reasons for your preference, considering aspects like security, transparency, and trust.
- If you have software development skills, write a program in your preferred language that implements the encryption and decryption process of your favorite symmetric cipher discussed in the lesson. Detail the procedure and challenges faced during implementation.
- Write an analysis comparing AES 128-bit and ChaCha20 256-bit. Discuss which you would prefer in terms of security and explain your reasoning.
- Explore encryption firsthand using online tools like Toolsou or Encode-Decode, practicing with algorithms such as AES, DES, and RC4.
If you learned something new today, help us to share it to reach others seeking knowledge.
If you have any queries or concerns, please drop them in the comment section below. We strive to respond promptly and address your questions.
Thank You
A finite field is a mathematical construct where a set of numbers is limited, and all arithmetic operations within the set result in a number that is also within the set. It is like a clock face representing a finite field of 12 hours; adding 4 hours to 10 o’clock gives you 2 o’clock, not 14 o’clock.
Galois Field (GF) and finite field refer to the same concept. A Galois Field, named after mathematician Évariste Galois is a type of finite field with a finite number of elements that is (2^8). It is a mathematical system where a limited set of numbers can be added, subtracted, multiplied, and divided (excluding division by zero), resulting in a new number within the same set. In AES, the finite field GF(2^8) means all operations are performed on bytes (8 bits long) and always produce a byte as a result, ensuring consistency within the encryption process.