Table of Contents

Welcome to our journey into the domain of Symmetric Key Cryptography. In this lesson, we will unravel the complications of how secret codes have evolved from ancient times to protect information in our increasingly connected world. Imagine sending a letter that only the intended recipient can read, despite it passing through many hands. That’s the essence of cryptography.
We’ll start with the basics of understanding how simple methods like Substitution, Permutation, and Transposition form the building blocks of encrypting messages. Explore the significance of XOR operations and the role of Initialization Vectors (IVs) in enhancing encryption security.
Our journey will also take you through the distinct differences between Stream and Block Ciphers, shedding light on their specific applications. Furthermore, we will explore various Block Cipher Modes, each with its unique mechanism and use case.
Designed for clarity and engagement, this lesson aims to connect you with the real-world applications of cryptography, making the complex understandable. Whether you’re new to cybersecurity or expanding your knowledge, this lesson will be a valuable step in your learning journey.
What is Symmetric Key Cryptography?
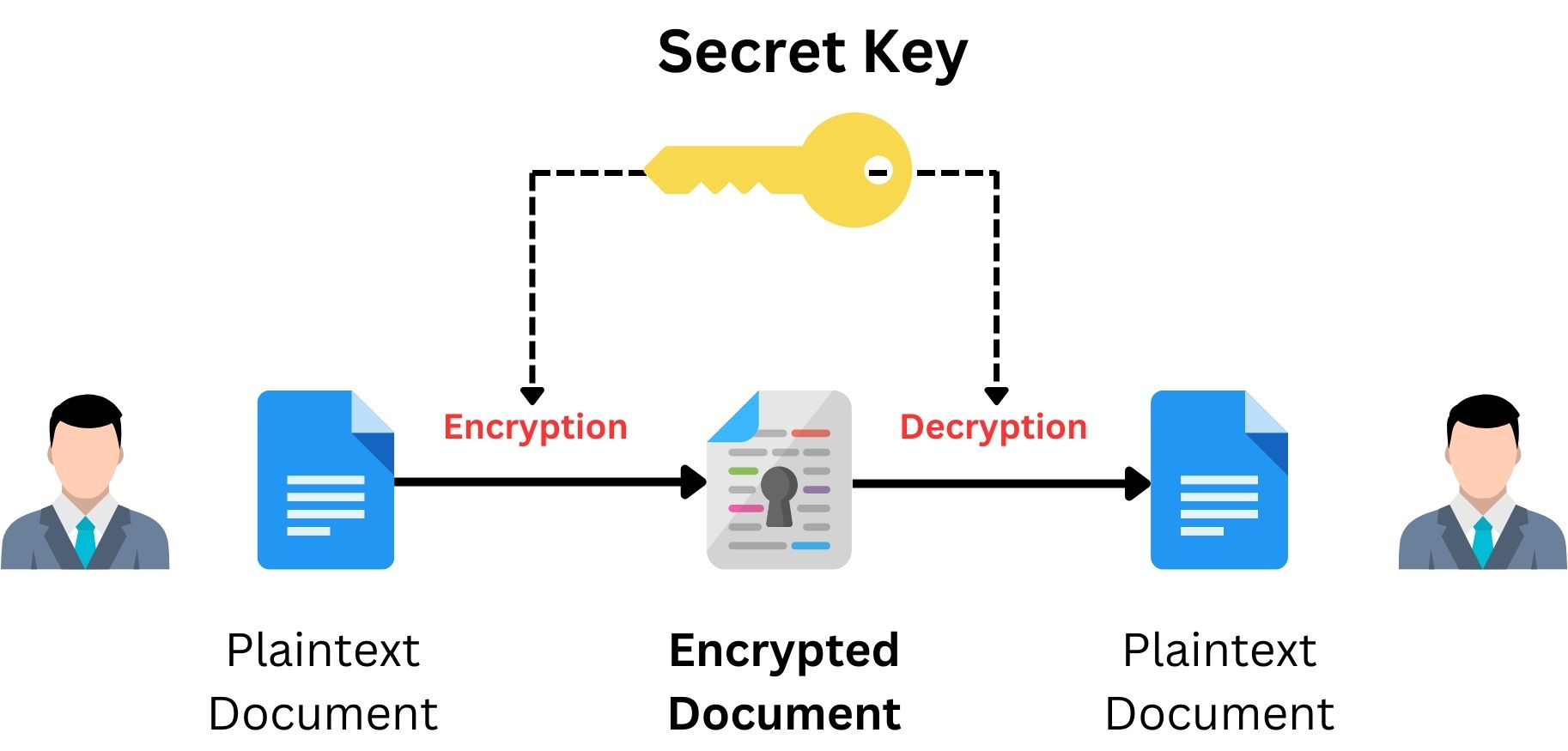
Symmetric Key Cryptography is a method used in cybersecurity to protect information. It’s like having a secret code that only the sender and receiver know. This code, called a “key”, and used to both lock (encrypt) and unlock (decrypt) the information. Imagine sending a locked box through the mail. If the person receiving it has the same key, they can open it. That’s how Symmetric Key Cryptography works. The concept is quite straightforward, the same key is used for both encrypting and decrypting data. This is different from Asymmetric Cryptography, where two different keys are used.
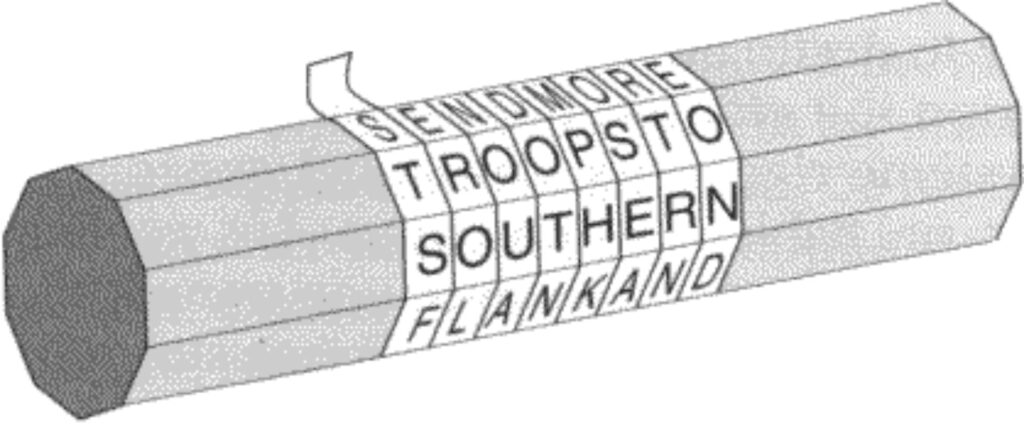
Symmetric Cryptography has been around for a long time. Its history dates back thousands of years, even to ancient civilizations. They used simple forms of symmetric encryption to protect secrets and messages. For example, in ancient Greeks used the Scytale, a cylindrical tool, for symmetric encryption. By wrapping a ribbon around the Scytale, they wrote a message across it. The recipient, with a cylinder of the same diameter, could wrap the ribbon and read the secret message.
However, in the digital age, this concept has become more sophisticated. Computers and advanced algorithms now create complex keys that are hard to guess or break. The technical history of Symmetric Cryptography in computer systems evolved significantly over time. Initially, it used basic substitution ciphers, but with advancing computing power, these became insufficient. The 1970s saw the introduction of the Data Encryption Standard (DES), a pivotal advancement using a 56-bit key. However, as DES’s vulnerabilities emerged, Triple DES was developed, enhancing security by applying DES three times to each data block. The early 2000s brought the Advanced Encryption Standard (AES), with key sizes up to 256 bits, offering superior security and efficiency. This evolution reflects Symmetric Cryptography’s adaptation to increasingly complex digital security needs.
Symmetric Encryption technology is widely used because it is faster and simpler in many cases than other methods. It’s especially useful when large amounts of data need to be encrypted quickly. However, it does have a challenge that both parties need to have the same key, and keeping this key secret is crucial. If someone else gets the key, they can access the encrypted information. This is why it’s important to use this method carefully and ensure the key is shared securely.
Substitution vs Permutation vs Transposition
There are three fundamental techniques used in Symmetric Cryptography to transform plaintext into ciphertext; substitution, permutation, and transposition. Substitution involves replacing characters with others, permutation rearranges them in complex patterns, and transposition shifts their positions in a more straightforward manner. These methods can be employed individually or combined, adding layers of complexity to encryption, thereby enhancing security and making the encoded message more resistant to unauthorized decryption.
Substitution
In Symmetric Encryption, Substitution is a method where elements of the plaintext (the original message) are systematically replaced or substituted with other characters, numbers, or symbols. It’s like changing the letters in a word to create a secret code. Each character in the plaintext is swapped with another character according to a predetermined system or key.
The working of substitution is quite simple yet effective. For example, in a basic substitution cipher, each letter of the alphabet could be replaced with another letter. A becomes D, B becomes E, and so on. This systematic replacement makes the original message unreadable to anyone who doesn’t know the substitution key. It’s a straightforward way to disguise information and is considered a basic form of encryption that, despite its simplicity, can be quite effective in certain contexts. It’s particularly useful when the volume of data is small, and the security requirement is not very high. However, in its simplest forms, it can be vulnerable to analysis and deciphering, especially with modern computational techniques.
A practical example to help you understand might be the classic “Caesar Cipher,” named after Julius Caesar, who reportedly used it. In this cipher, each letter in the plaintext is shifted a certain number of places down the alphabet. If the shift is three places, then A becomes D, B becomes E, and so on. Thus, the word “HELLO” becomes “KHOOR.” It’s a straightforward yet clear example of how substitution alters the original message to keep it secure from unintended recipients.
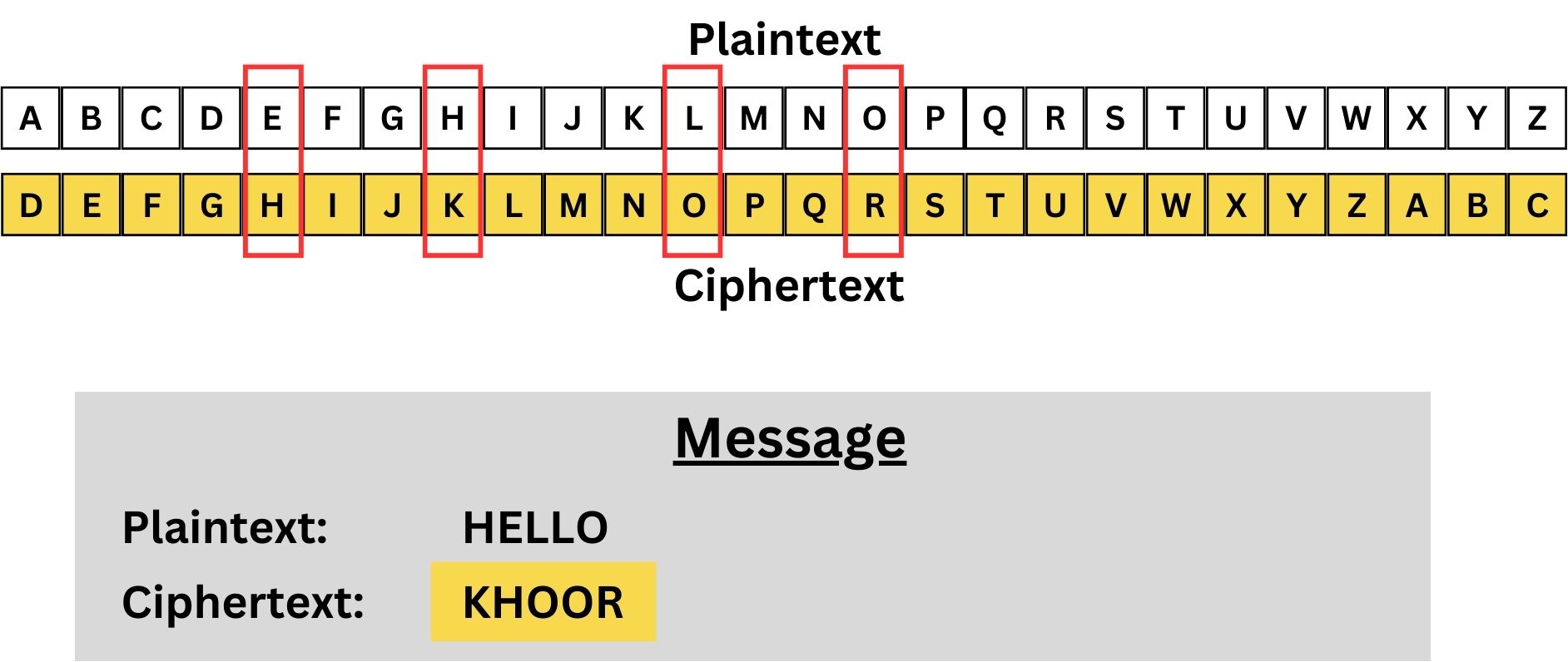
The key is the number of shifts, which is three in this case. This means every letter in the plaintext is shifted three places down the alphabet.
It’s important to note that the Caesar Cipher is an extremely simplified example of substitution in cryptography. In actual cybersecurity applications, the complexity of substitution techniques is far greater. Modern substitution ciphers use intricate algorithms and larger sets of characters, making them much more resistant to decryption attempts. This increased complexity ensures a higher level of security, essential in protecting sensitive digital information in today’s technologically advanced environment.
Permutation
Permutation involves rearranging the characters or bits of the plaintext (original message) in a specific order, determined by a key. Unlike substitution, which replaces characters, permutation shuffles them. It’s like rearranging the pieces of a puzzle; the pieces themselves don’t change, but their positions do.
It is straightforward and effective in creating confusion. The positions of characters or groups of characters are shuffled according to a predefined pattern or key. This process transforms the plaintext into a jumbled version, known as ciphertext, which appears random and incomprehensible without knowledge of the permutation key. Permutation can be used to add another layer of complexity to the encryption process besides substitution, enhancing the overall security of the encryption.
A simple example to illustrate permutation is the Rail Fence Cipher. In this technique, the plaintext is written in a zigzag pattern across multiple lines, and then read off line by line. For instance, the message “HELLO WORLD” can be split across two lines: HLOOL ELWRD. Reading these lines sequentially gives the ciphertext: HLOOLELWRD. This example, while basic, demonstrates how rearranging the characters in a specific order can effectively scramble a message, an essential concept in more complex cryptographic permutations.
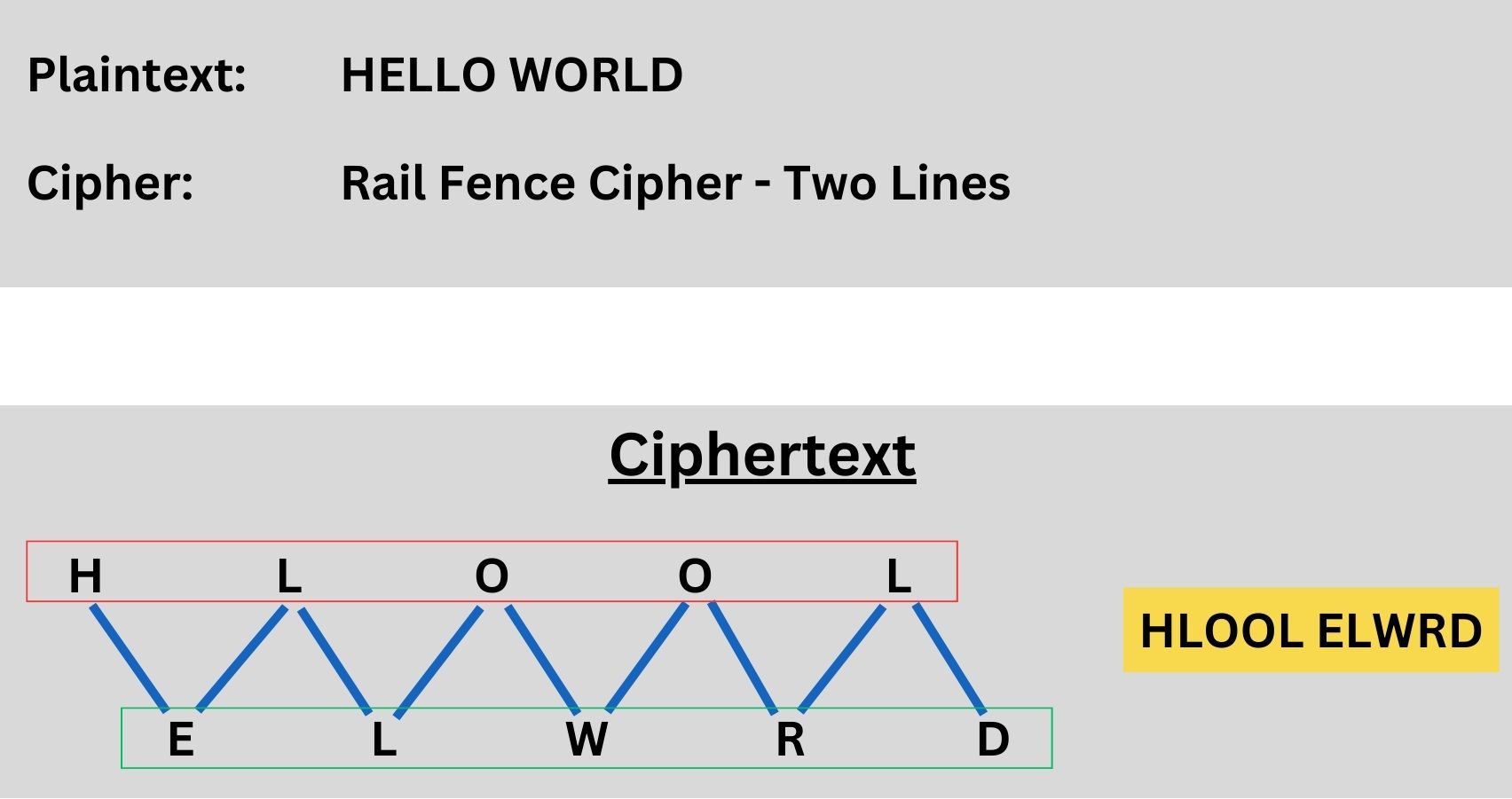
Remember, while this is a simple representation, real-world cryptographic permutations are much more complex and secure. We chose two lines for the Rail Fence Cipher example to keep it simple and easy to understand. With two lines, the zigzag pattern is more straightforward, making the concept of permutation clearer, especially for those new to cryptography. Three lines would add complexity, potentially obscuring the basic idea of how permutation works. Other algorithms like AES and DES also use permutations, such as AES’s ‘ShiftRows’ and DES’s initial and final permutations, but these are more complex and provide higher security in real-world applications.
Transposition
Transposition is a technique where the positions of characters or groups of characters in the plaintext (the original, unencrypted message) are shuffled according to a specific system or key. Unlike substitution, which replaces characters with others, or permutation, which rearranges them in a complex pattern, transposition is more about changing the order of existing characters in a straightforward manner.
The process works by taking the plaintext and rearranging its characters based on a predetermined rule or key. For instance, in a simple transposition cipher, characters might be swapped in pairs, or the message might be written in rows and then read off in columns.
A classic example of transposition is the Columnar Transposition. In this method, the plaintext is written out in rows of a fixed length, and then the columns are transposed based on a key. For instance, consider a plaintext message “HELLO WORLD” with a key of 3124. Since the key has 4 digits, you divide the plaintext into columns of 4 characters each. The grid will look like this:

Note the two empty spaces in the last row. In real-world scenarios, padding algorithms are used adding extra characters.
Now, rearrange the columns based on the order of the numbers in the key. So, the column under “1” goes first, then “2”, and so on. Rearranged grid becomes:

The columns are now in the sequence 1-2-3-4. Read the letters in columns from top to bottom and left to right, skipping the empty spaces. Ciphertext is “EWDLORHOELL“
Please note that the examples we’re using to illustrate cryptographic techniques like substitution, permutation, and transposition are intentionally simplistic. They’re designed to help you understand the basic concepts. We’re not considering complexities like dealing with spaces or incorporating padding algorithms in these examples. These are just starting points for learning.

Exclusive OR (XOR)
Exclusive OR (XOR) is a fundamental operation in Symmetric Key Cryptography, known for its simplicity and effectiveness. At its core, XOR is a logical operation that compares two bits (binary digits). The rule of XOR is straightforward; if the two bits are different, it outputs 1; if they are the same, it outputs 0. This property makes XOR particularly useful in cryptography.
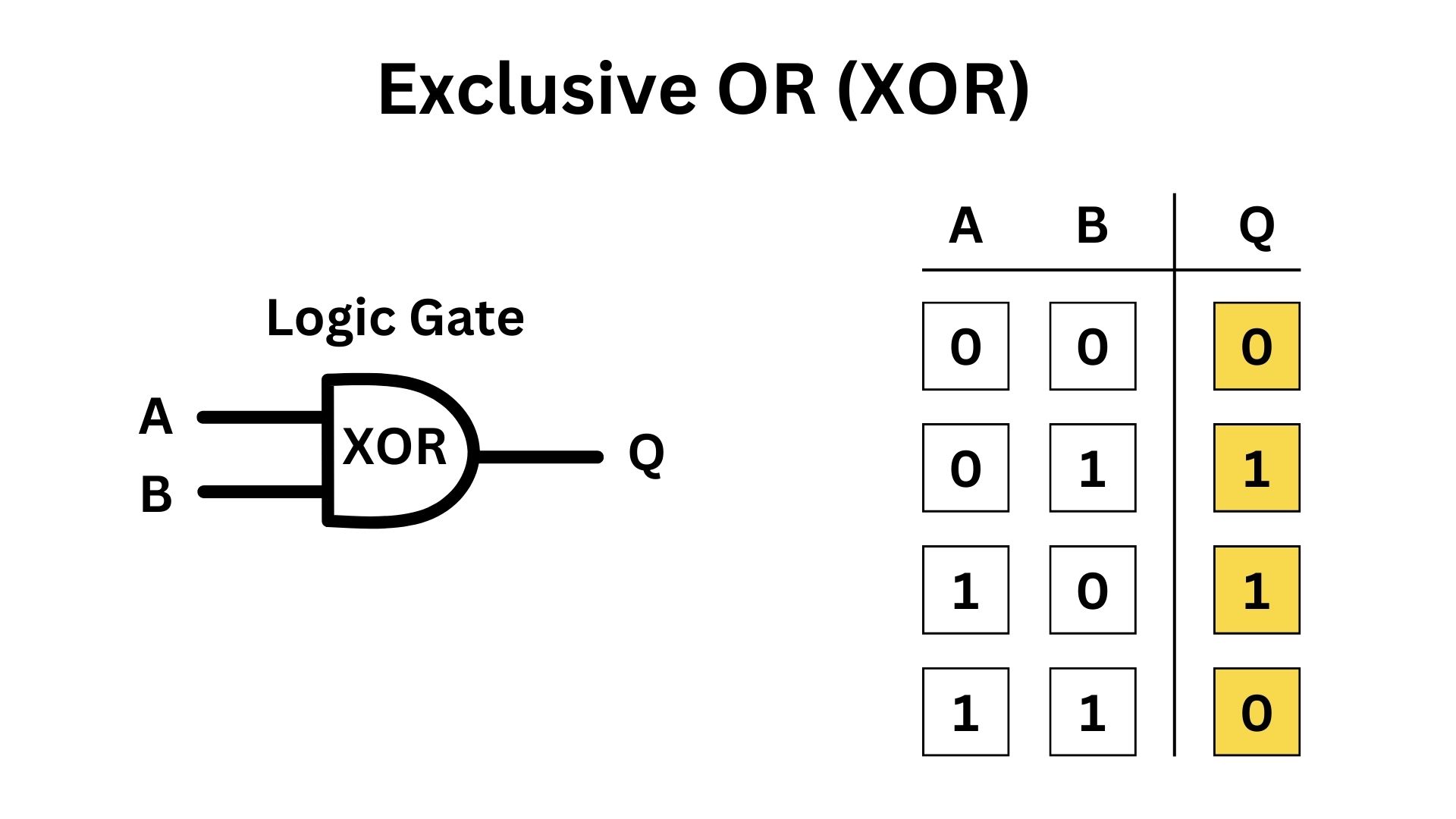
In the context of cryptography, XOR is used to combine the plaintext with a key. Each bit of the plaintext is XOR-ed with the corresponding bit of the key. If the plaintext bit and the key bit are different, the output is 1; if they’re the same, the output is 0. This process creates the ciphertext, which appears as a random string of bits to anyone who doesn’t have the key. XOR’s importance in cryptography lies in its reversibility and simplicity. The same XOR operation is used for both encryption and decryption. If you XOR the ciphertext with the same key, you get back the original plaintext. This reversibility is crucial in symmetric cryptography, where the same key is used for both encrypting and decrypting data.
One of the reasons XOR is chosen over other logical operations is its non-linearity. Unlike AND or OR operations, XOR doesn’t favor 0s or 1s; it treats them equally, which is important for maintaining the randomness of the ciphertext. Additionally, XOR doesn’t reveal much about the input from the output, which is a desirable property in cryptography to prevent attacks based on analyzing the encrypted data.
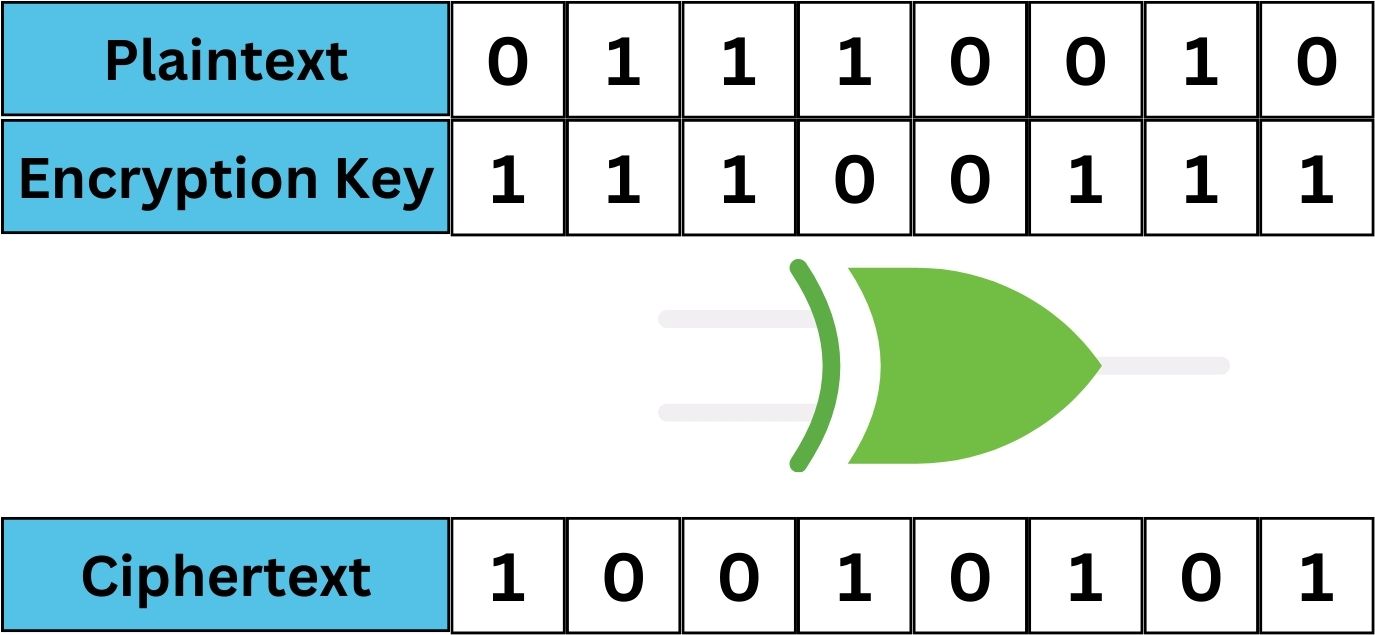
To demonstrate XOR in a practical example, let’s consider a plaintext ‘HELLO’ and a key ‘XMCKL’. First, we convert each character to its binary form:
HELLO: 01001000 01000101 01001100 01001100 01001111
XMCKL: 01011000 01001101 01000011 01001011 01001100
Now, we XOR these binary strings:
Result: 00010000 00001000 00001111 00000111 00000011
Converting this result back to characters, we get the encrypted ciphertext. The simplicity and effectiveness of XOR in altering the plaintext while allowing for easy decryption with the same key make it a valuable tool in symmetric cryptography.
Initialization Vector (IV)
The Initialization Vector (IV) is a critical concept in Symmetric Key Encryption, particularly when using encryption methods like block ciphers (we will cover it next). An IV is essentially a block of bits used alongside the secret key to initialize the encryption process. It’s not a secret itself, but it adds an extra layer of complexity to the encryption. The primary role of an IV is to ensure that the same plaintext encrypted multiple times with the same key produces different ciphertexts. This is crucial for security because if the same plaintext always resulted in the same ciphertext, it could give attackers clues about the encrypted messages. IVs prevent this by providing an element of randomness in each encryption operation.
But why do we need an IV if we already have the XOR process? While XOR is effective in altering the plaintext, it has a limitation; when the same plaintext and key are used, it produces the same ciphertext every time. This predictability can be exploited in certain types of cryptographic attacks. For example, if an attacker knows that a particular plaintext always encrypts to a certain ciphertext, they can start to deduce information about the key or other plaintexts.
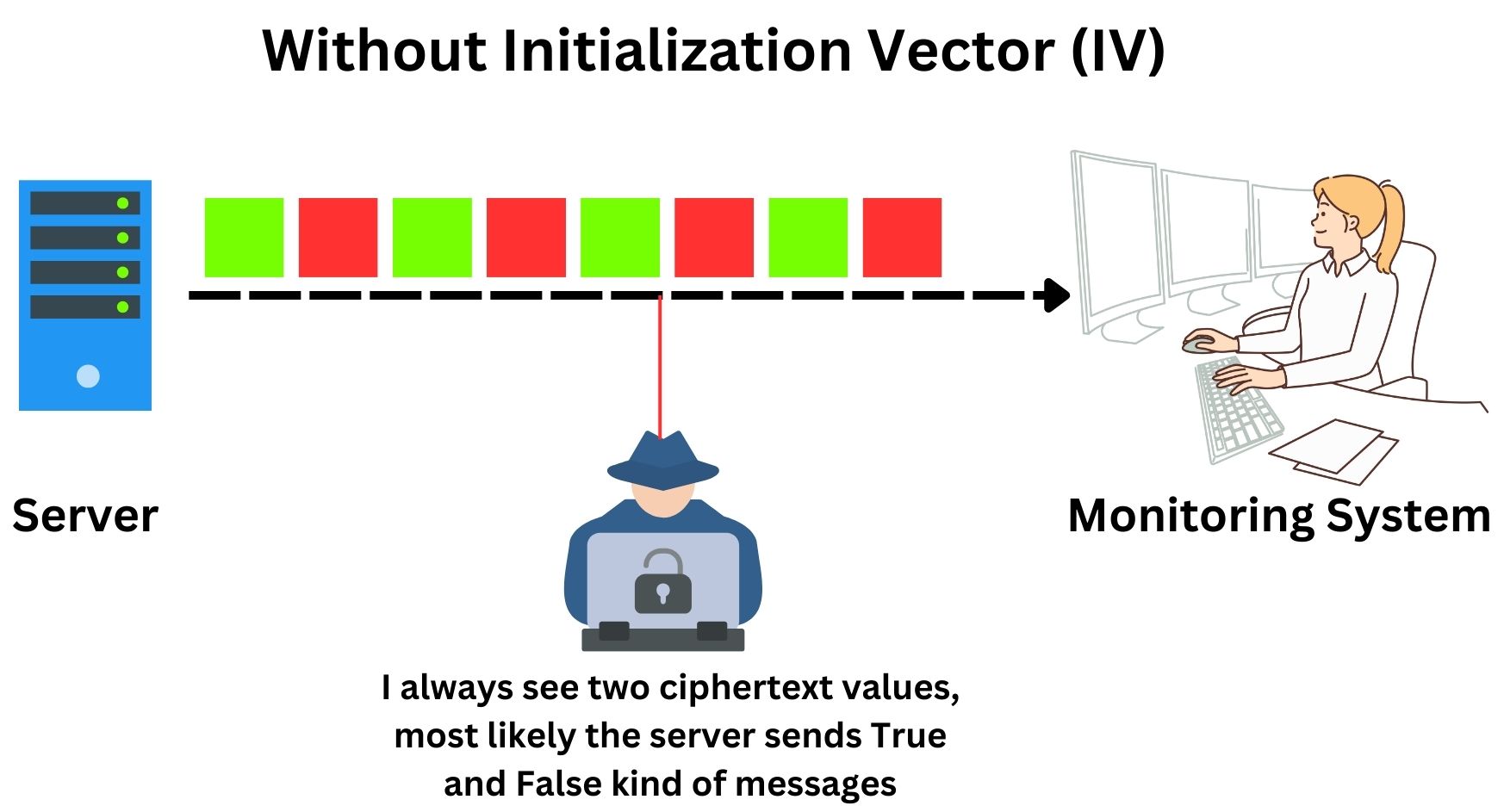
Consider an enterprise server system that regularly sends status updates to a central monitoring dashboard, indicating “Server Running” (True) or “Server Down” (False). In the absence of an IV, each “True” or “False” status, when encrypted with the same key, would always generate identical ciphertexts. This consistency could be exploited by attackers to infer system patterns or identify vulnerabilities.
However, when an IV is utilized, each “True” or “False” message is combined with a unique IV before encryption. This ensures that even if the server status remains the same and is transmitted repeatedly, the encrypted messages (ciphertexts) appear different each time. This diversity in ciphertexts, despite the repetition of actual server statuses, even if the same True and False messages are repeated a billion times, from a ciphertext perspective they will look completely different each time, significantly enhances security and preventing potential attackers from deducing patterns or predicting server behaviors.
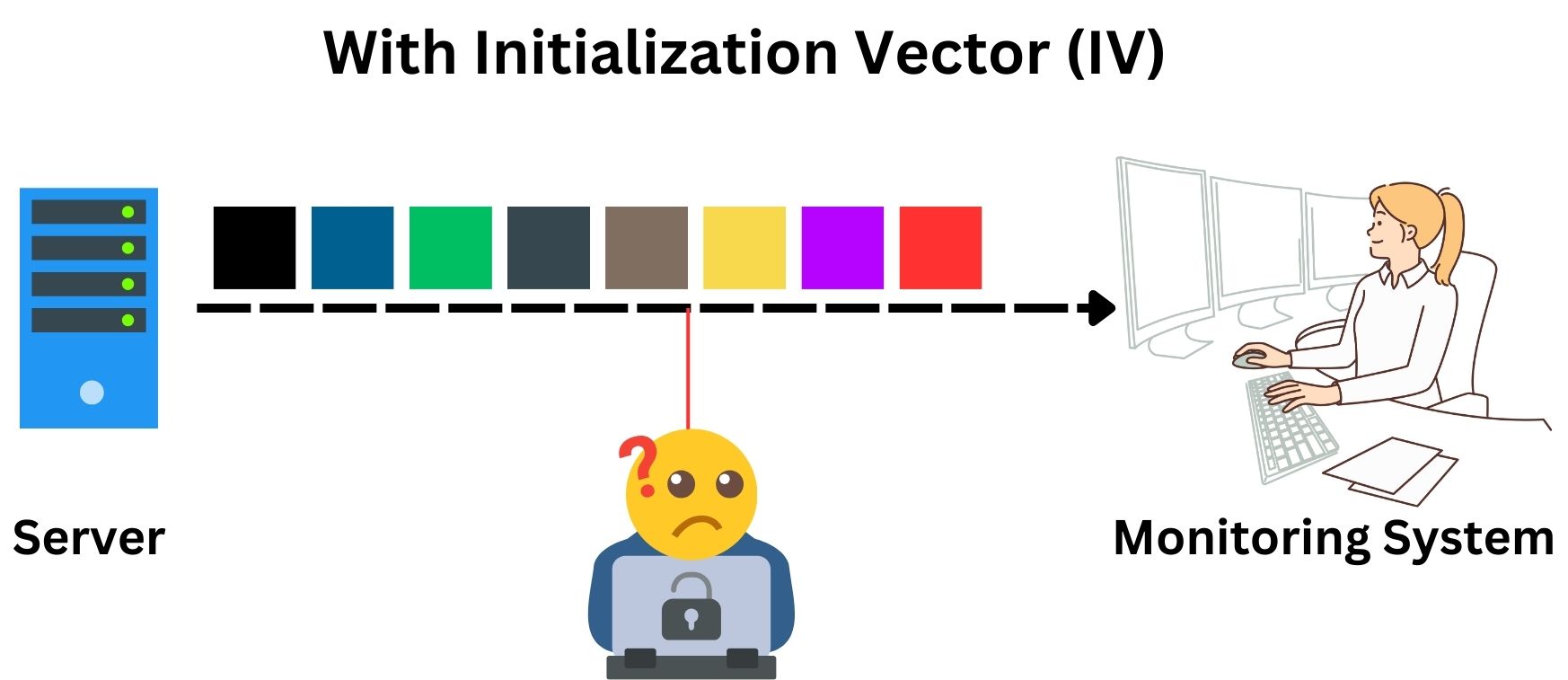
The IV addresses this issue by adding randomness to the process. Before the XOR operation, a unique IV value is generated and combined with the plaintext, typically also using XOR. This means that even if the same plaintext and key are used, the presence of a different IV each time results in a unique ciphertext. In the following image, we trying to illustrate the process of encrypting the word “NO” where the binary value is:
01001110 01001111.
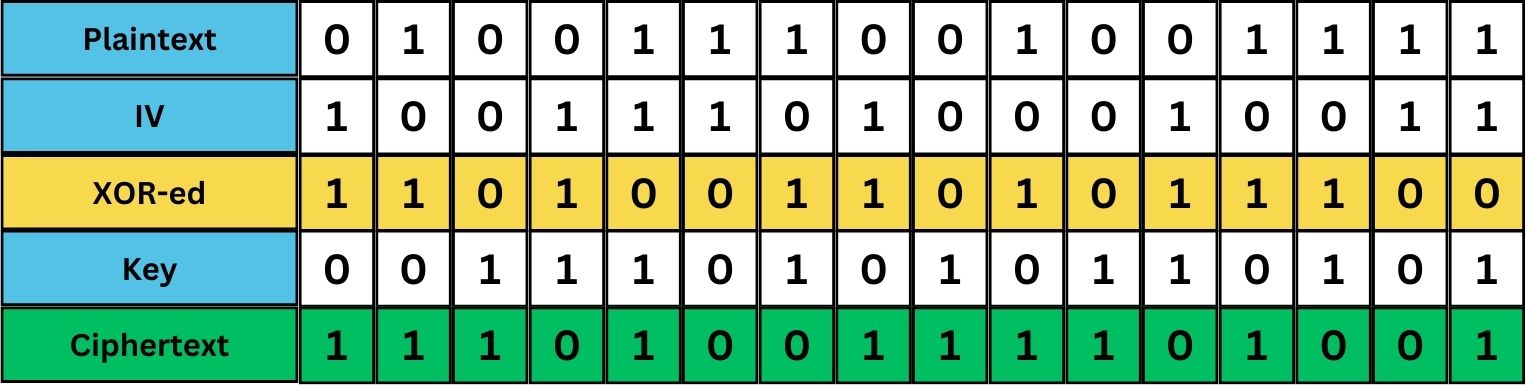
If you try it yourself to encrypt the same binary and use a new and unique IV value, it will result in a different ciphertext, even though the plaintext message is exactly the same.
How does the recipient get to know about the IV value used by the sender?
In practice, the recipient needs to know the IV to decrypt the message, but the IV doesn’t have to be kept secret like the key. Typically, the IV is sent along with the ciphertext. It’s often placed at the beginning of the encrypted data. Since the IV’s purpose is to provide randomness and not secrecy, its exposure doesn’t compromise the security of the encrypted message. Upon receiving the message, the recipient uses this IV along with their secret key to decrypt the ciphertext, ensuring they can accurately retrieve the original plaintext.
Quick Quiz
Stream Cipher vs Block Cipher
Before diving into the specifics of Stream Ciphers and Block Ciphers, it’s important to understand why we consider different types of encryption methods in cryptography. Encryption isn’t a one-size-fits-all solution; different scenarios and requirements call for different approaches. The choice between a Stream Cipher and a Block Cipher depends on factors like the size of the data, the need for speed and efficiency, the context of data transmission, and the level of security required.
Stream Cipher
A Stream Cipher is a type of encryption method used in Symmetric Cryptography. It encrypts plaintext data one bit or one byte at a time, in a continuous stream. The encryption happens on-the-fly as the data flows through the encryption algorithm.
In stream cipher encryption, the plaintext is combined with a pseudorandom cipher digit stream (key stream), typically using an operation like XOR. Each bit or byte of the plaintext is encrypted by a corresponding bit or byte from the key stream, producing ciphertext. The key stream is generated based on a secret key, ensuring that only a recipient with the correct key can decrypt the message.
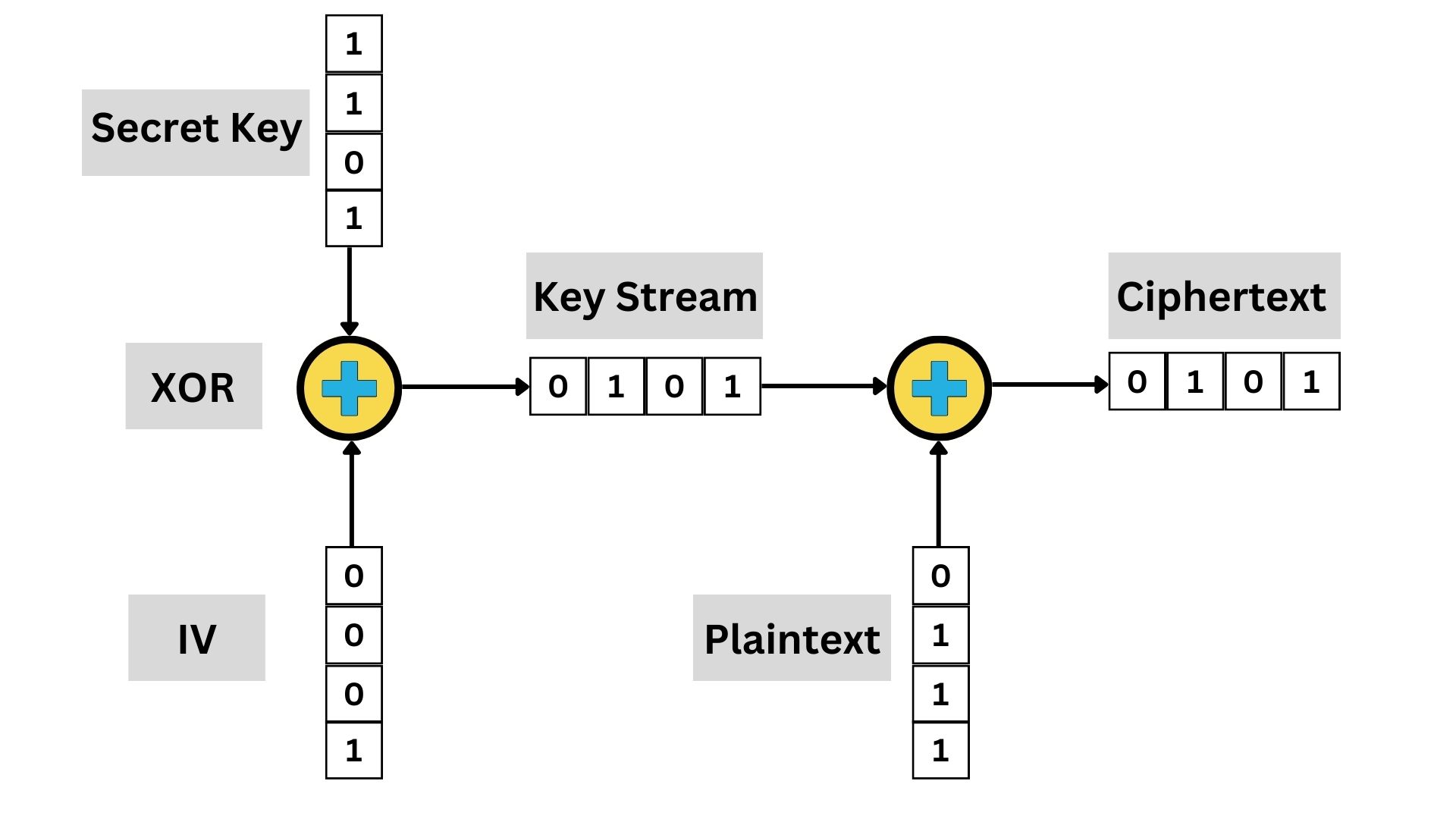
the security of a stream cipher heavily relies on the quality of the key stream; any predictability or repetition in the key stream can lead to vulnerabilities. Thus, the design of secure stream ciphers requires careful attention to the generation of a key stream that is as random and unpredictable as possible.
Pros of Stream Ciphers:
- Stream Ciphers are generally faster and more efficient for real-time data encryption, like in live voice or video streaming, because they process data incrementally.
- They can handle data streams of varying lengths without needing padding or adjustments, making the process very flexible.
- Ideal for applications where quick data processing is crucial, ensuring minimal delay and low latency.
Cons of Stream Ciphers:
- The security of a Stream Cipher heavily relies on the key; reusing a key can be particularly risky and can compromise the encryption.
- Since encryption is sequential, any error in the transmission can affect the decryption process.
Block Cipher
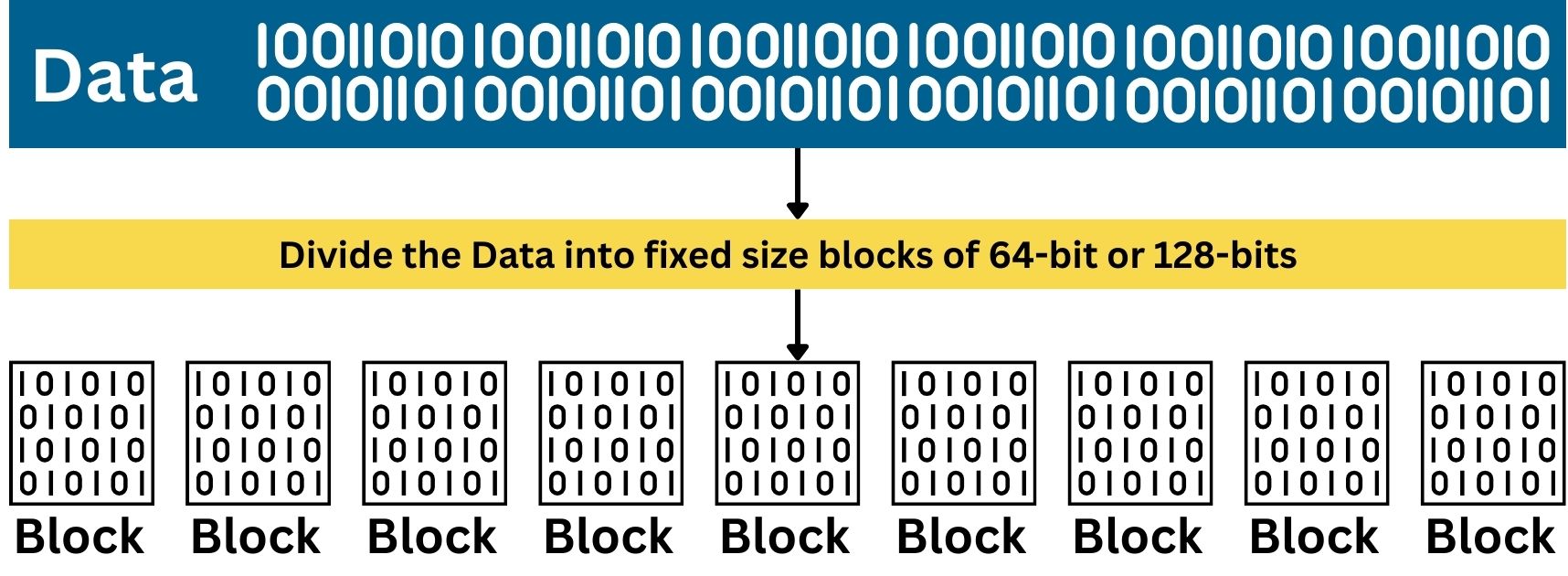
Like Stream Cipher, Block Cipher is a type of encryption method in Symmetric Cryptography, however, it works in a completely different way. It processes data in fixed-size blocks, typically of 64 or 128 bits. Each block of plaintext is encrypted as a single unit, transforming it into a block of ciphertext using a specific key. Unlike Stream Ciphers, which encrypt data bit by bit, Block Ciphers work on these larger, consistent blocks of data.
Before encryption, the plaintext data is divided into blocks of a fixed size. If the last block is not long enough to fill the block size, it’s padded to reach the required length. This padding ensures that each block can be processed uniformly.
The block cipher uses the secret key to generate a series of round keys through a process called Key Scheduling. The number of rounds and the complexity of key generation vary depending on the specific cipher. For example, AES-128 uses 10 rounds of encryption, each with its own round key derived from the original secret key. Each block of plaintext is then encrypted through a series of well-defined steps or rounds. Each round typically involves several operations, including substitution, permutation, transposition, mixing, and transformation, all designed to increase the security of the cipher.
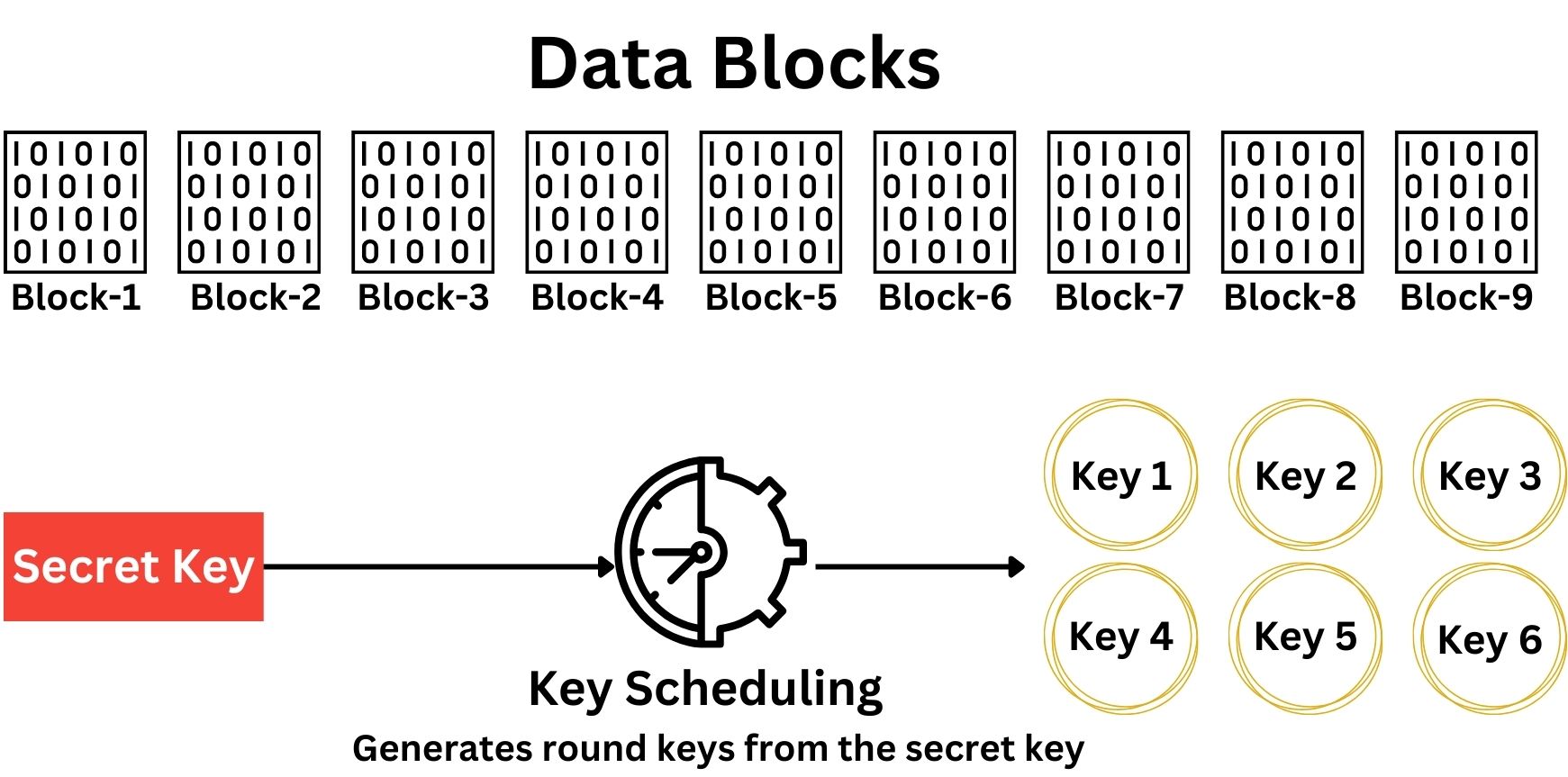
The round keys generated during the Key Scheduling process are unique for each round of encryption. The Key Scheduling algorithm takes the original secret key and systematically transforms it to produce a distinct round key for each encryption round. This ensures that every round applies a different cryptographic transformation, enhancing the security of the Block Cipher.
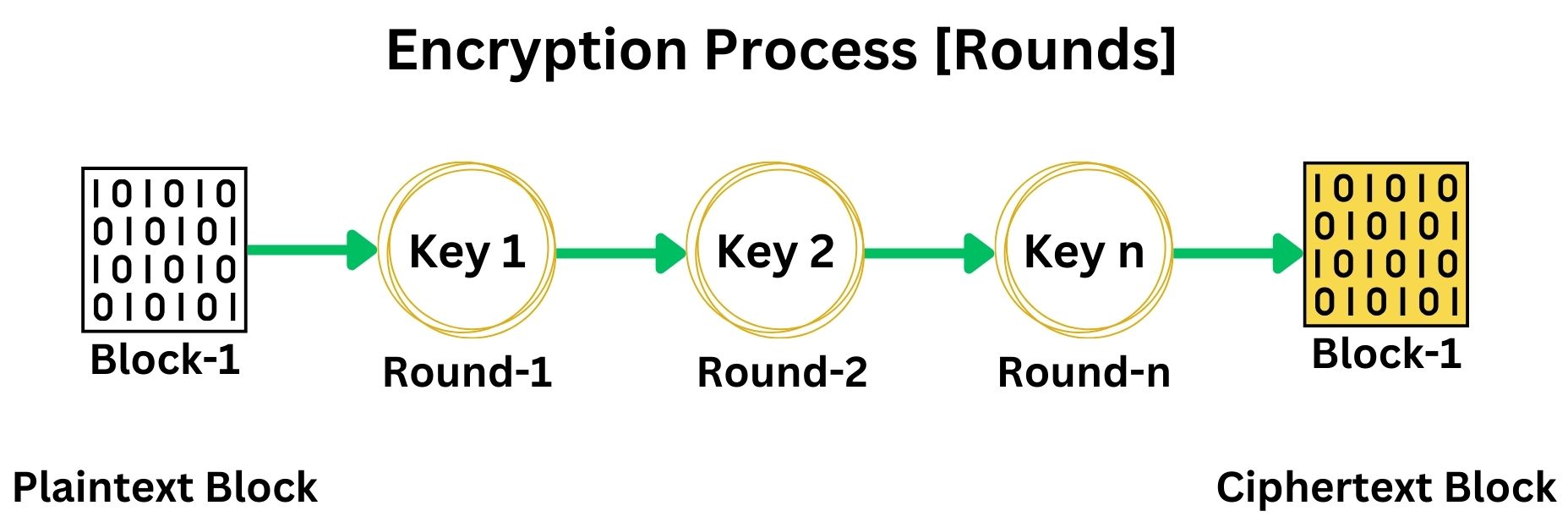
The output after the last round of encryption is an encrypted block, known as a cipher block. Each block of plaintext data is transformed through these rounds, using different round keys, into a secure and scrambled version. This process ensures the data’s confidentiality.
In block ciphers, transformation is a complex and integral step, involving a series of sophisticated mathematical and algorithmic operations applied to data during each encryption round. These operations typically include bitwise functions like XOR, and more intricate ones involving modular arithmetic or non-linear transformations. Their main objective is to intertwine the plaintext and key material, ensuring that even minor changes in either result in significant, unpredictable variations in the ciphertext. This process is crucial for achieving both diffusion and confusion; diffusion spreads the influence of a single plaintext bit across many ciphertext bits, while confusion obscures the relationship between the key and ciphertext. Such transformations are designed to be computationally efficient yet cryptographically robust, providing a strong defense against cryptanalysis.
After the last round, a final transformation is applied to produce the ciphertext block. This transformation is typically a simpler operation, ensuring that the last round’s output is sufficiently obscured.
To decrypt, the recipient uses the same secret key that was used for encryption. This secret key undergoes the Key Scheduling process in reverse to generate the same set of round keys that were used for encryption. The decryption process then applies these round keys in reverse order, undoing each round of encryption step-by-step. Since both the encryption and decryption processes are based on the same original secret key and follow the same Key Scheduling algorithm (just in reverse for decryption), the recipient can accurately reconstruct the plaintext from the ciphertext using the correct key.
Note that, in Block Cipher encryption, the round key size should typically match the block size. So, if you’re using a 64-bit block size, the round keys generated for each round should also be 64 bits in length. This ensures that the round key can be properly applied to each block during the encryption and decryption processes.
The number of round keys that can be generated in any block cipher algorithm, is determined by the cipher’s design, not just the key length. For instance, in AES-128, regardless of the key’s length (128 bits), the algorithm is designed to generate a specific number of round keys; 10 for AES-128. This is a fixed aspect of the AES algorithm and is not dependent on the number of possible combinations within the key length itself. If you provide the same secret key to five different AES-128 systems, each system will generate exactly the same 10 round keys. The Key Scheduling process in AES is deterministic, meaning it will always produce the same set of round keys from a given secret key.
The security of a block cipher relies on the complexity of these operations and the secrecy of the key. A well-designed block cipher is resistant to various types of cryptographic attacks, such as differential and linear cryptanalysis. The choice of block size, key size, and the number of rounds are crucial factors in determining the strength of a block cipher.
Pros of Block Ciphers:
- Block Ciphers are generally considered more secure than Stream Ciphers. The fixed block size allows for the implementation of complex and robust encryption algorithms.
- There is a wide variety of design principles and modes of operation that can be used with Block Ciphers, enhancing their versatility and security.
- Errors in a ciphertext block do not propagate; they typically affect only the corresponding block of plaintext upon decryption.
Cons of Block Ciphers:
- Block Ciphers can be slower compared to Stream Ciphers, especially when dealing with small amounts of data, due to the need to process entire blocks.
- If the plaintext doesn’t perfectly fit into a block, padding is required, which can add complexity and slight inefficiencies.
In Asymmetric Encryption, the concept of Stream and Block Ciphers is not applicable because the fundamental mechanisms and purposes of Asymmetric Encryption differ significantly from those of Symmetric Encryption. Asymmetric Encryption, also known as Public Key Cryptography, involves two distinct keys: a public key for encryption and a private key for decryption. Its primary use is secure key exchange and authentication, rather than bulk data encryption. This method relies on mathematical functions based on hard-to-solve problems, like prime factorization, which don’t operate on the principles of streaming or blocking data. In contrast, Symmetric Encryption, where the same key is used for both encryption and decryption, is designed for efficiently processing large amounts of data, making concepts like Stream and Block Ciphers relevant and necessary for handling data in different scenarios, whether in a continuous stream or in fixed-size blocks. These differing objectives and operational modes explain why Stream and Block Ciphers are specific to Symmetric Encryption.
The following table compares Stream Cipher and Block Cipher across various criteria. It highlights the key differences between Stream and Block Ciphers across various aspects, helping in understanding their distinct characteristics and suitable applications.
| Criteria | ECB | CBC | CFB | OFB | CTR |
|---|---|---|---|---|---|
| Function | Encrypts each block separately. | Chains blocks together. | Encrypts segment-wise, influenced by previous ciphertext. | Encrypts IV, independent of plaintext. | Encrypts counter value for keystream. |
| Data Dependency | None (blocks are independent). | Each block depends on the previous one. | Each segment depends on the previous ciphertext. | Independent of plaintext and ciphertext. | Independent of plaintext and ciphertext. |
| Error Propagation | Limited to one block. | Affects two blocks. | Affects subsequent segments. | No error propagation. | No error propagation. |
| Parallel Processing | Yes. | No. | No. | Yes. | Yes. |
| IV Requirement | Not required. | Required. | Required. | Required. | Required. |
| Use Case | Simple, less secure scenarios. | General purpose. | Streaming data with variable lengths. | Streaming data with error resilience. | High-speed or parallel processing needs. |
| Key Feature | Simplicity. | Security via chaining. | Flexibility in data length. | Keystream generation. | Counter-based keystream. |
| Padding Requirement | Required if data doesn't fit block size. | Required if data doesn't fit block size. | Not required, flexible segment sizes. | Not required, independent of plaintext size. | Not required, can process data of any size. |
Block Cipher Modes of Operation
Before delving into Block Cipher Modes of Operation, it’s essential to understand that these modes determine how block ciphers process plaintext and ciphertext. Each mode offers a unique approach to encryption, balancing factors like security, efficiency, and data integrity. Understanding these modes is crucial in selecting the right one for specific encryption needs, as they profoundly impact the overall security and functionality of the cryptographic process.
Stream ciphers encrypt data bit by bit or byte by byte in a continuous stream, inherently incorporating the mode within their operation. Therefore, stream ciphers don’t require separate modes to manage data blocks, as their continuous, sequential nature inherently dictates their mode of processing data.
Modes of operation are needed only in block ciphers because they process fixed-size blocks of data, and different modes provide various methods to handle these blocks securely and effectively.
Electronic Codebook (ECB)
It encrypts each block of plaintext separately using the same key, leading to identical ciphertext blocks for identical plaintext blocks. Its simplicity and parallelizability are key features, allowing easy implementation and independent processing of each block. However, its major weaknesses include predictability and lack of security; the absence of an Initialization Vector (IV) or chaining results in patterns that are vulnerable to exploitation, and identical plaintext blocks create identical ciphertexts, making ECB susceptible to replay attacks. This makes ECB less suitable for data with repetitive information or patterns, highlighting its limitations despite its straightforward approach.
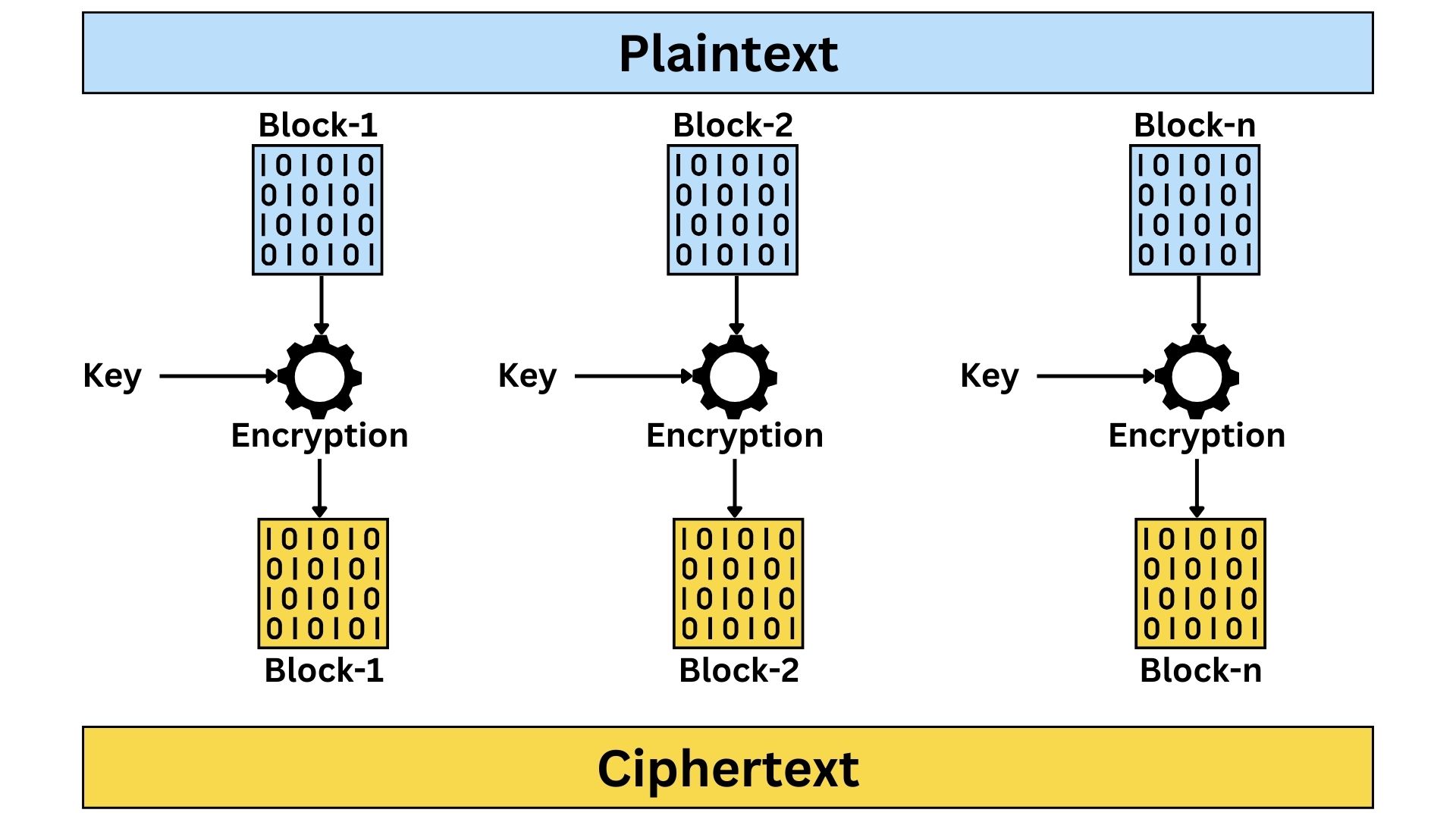
Cipher Block Chaining (CBC)
Widely used encryption method in block ciphers, enhances security by incorporating each encrypted block’s output into the encryption of the next block. It begins with an Initialization Vector (IV) for the first block, and each subsequent block of plaintext is XOR-ed with the previous block’s ciphertext before being encrypted. This method ensures that identical plaintext blocks result in different ciphertexts, significantly improving security over ECB. However, CBC requires sequential processing, which can slow down encryption and decryption. An error in one ciphertext block can also corrupt the corresponding plaintext block and the next one during decryption. Despite these challenges, CBC’s strength lies in its ability to obscure patterns in data, making it more secure and suitable for a wider range of encryption needs.
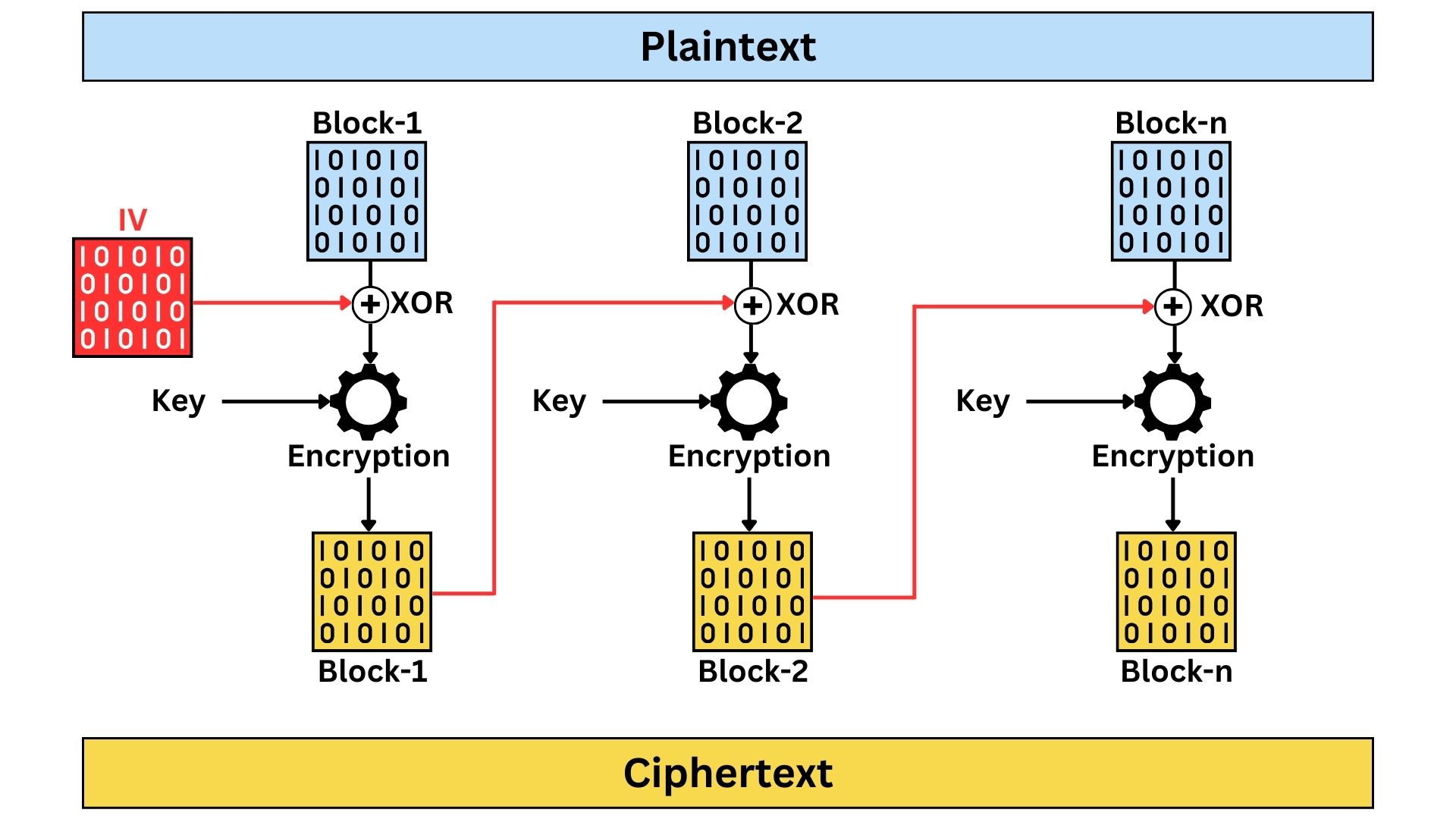
In CBC mode, the Initialization Vector (IV) is treated as a block, similar in size to the other blocks of plaintext. It is not used in a stream manner. The IV is XOR-ed with the first block of plaintext before encryption, starting the chaining process that characterizes Cipher Block Chaining. This block-sized IV ensures consistency with the encryption process of the subsequent data blocks.
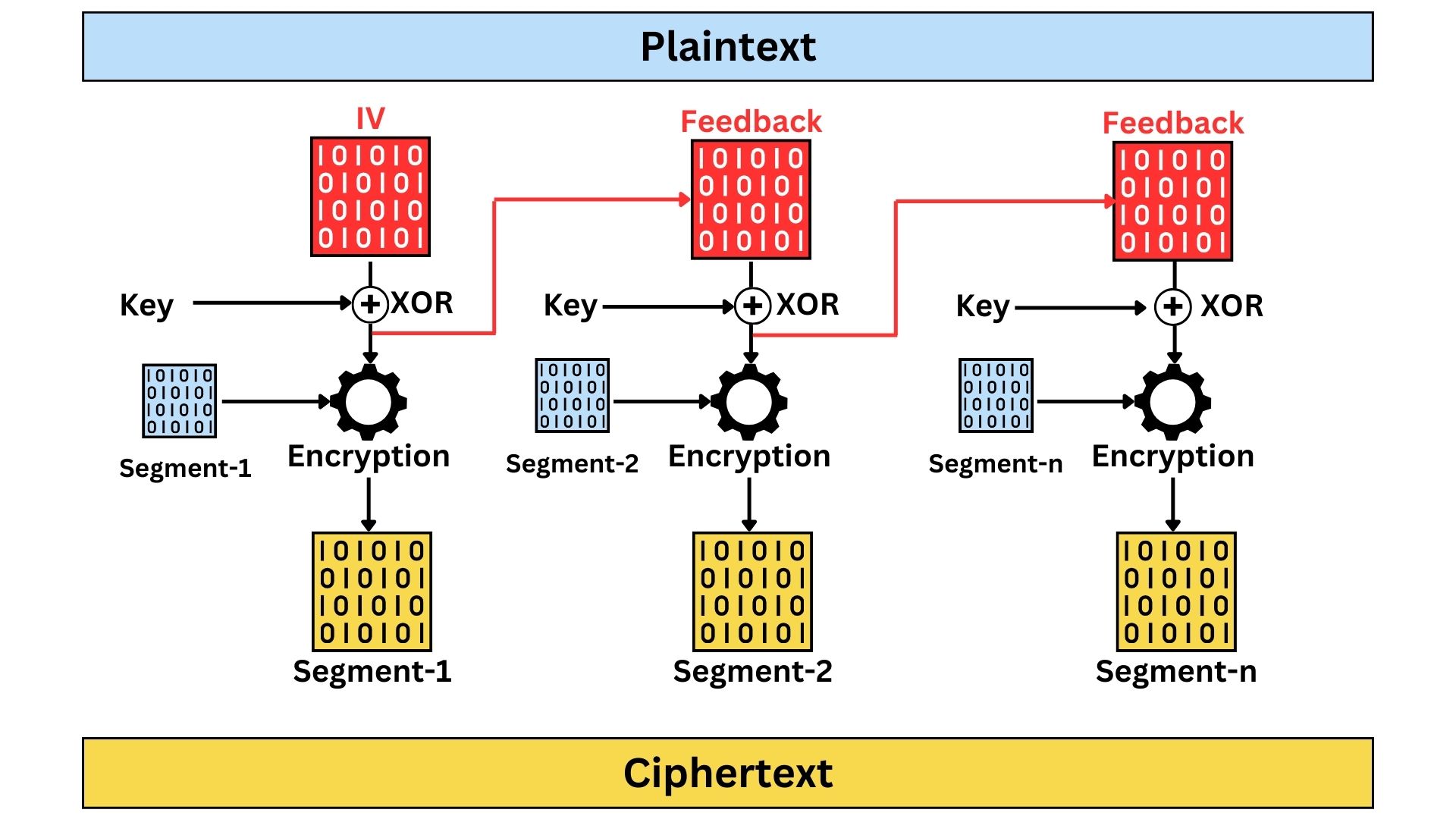
Cipher Feedback (CFB)
CFB allows data to be encrypted in units smaller than the block size called “segments”, making it function similarly to a stream cipher. The size of the segments in Cipher Feedback (CFB) mode is not fixed by any standard and can be chosen based on the specific requirements of the application. It can range from a single bit to the full size of the block. This flexibility allows CFB to be tailored for different data lengths and use cases, offering versatility in how data is encrypted.
The process starts by encrypting an Initialization Vector (IV) with the encryption key, and then the output is XOR-ed with the segments of the plaintext to produce the ciphertext.
For encrypting the next segment, the ciphertext (encrypted segment) whether all of it or part of it (depends on configuration) is then taken and used as feedback. This feedback gets encrypted again with the key and the output generated is XOR-ed with the next plaintext segments to produce the next piece of ciphertext.
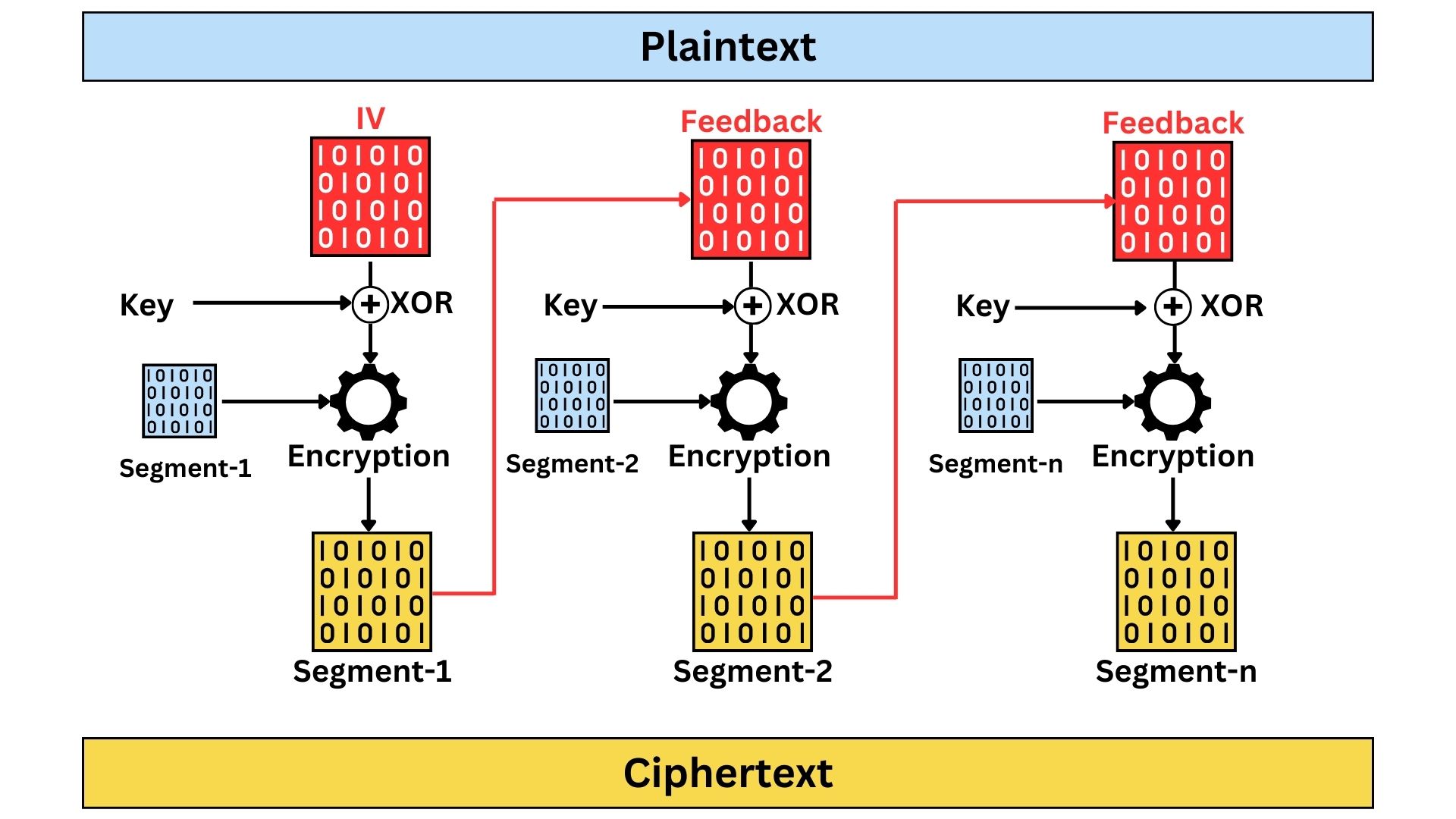
This feedback mechanism allows for the encryption of data in segments smaller than the block size, offering flexibility and making CFB suitable for streaming data. While CFB provides better security than ECB by obscuring patterns in the data, it is susceptible to error propagation; an error in a ciphertext segment can affect the subsequent segments. Its sequential nature also means that parallel processing isn’t possible, potentially slowing down the encryption and decryption processes. Despite these limitations, CFB’s ability to handle data in varying lengths without padding makes it a versatile choice in certain applications.
Output Feedback (OFB)
Output Feedback (OFB) mode is a block cipher mode of operation that turns a block cipher into a synchronous stream cipher. It generates keystream blocks, which are then XOR-ed with the plaintext blocks to produce ciphertext. OFB differs from other modes like CBC or CFB in that it focuses on encrypting a repeatedly processed Initialization Vector (IV) rather than the plaintext or ciphertext directly.
In OFB, the IV is first encrypted using the block cipher. The output of this encryption is then used as the keystream. This keystream is XOR-ed with the plaintext to create ciphertext. For the next block, instead of using the ciphertext, OFB re-encrypts the previous encryption output. This process continues, with each new output feeding back as the input for the next block’s encryption.
Output Feedback (OFB) mode excels in its resilience to transmission errors, as errors in ciphertext do not affect plaintext, and its ability to pre-generate keystream blocks, enhancing encryption speed. However, it requires strict synchronization between sender and receiver to maintain decryption integrity, and each encryption session must use a unique IV for security. These features make OFB suitable for specific scenarios where data integrity and error resilience are paramount.
Counter (CTR)
Counter (CTR) mode is like OFB, which turns a block cipher into a stream cipher. It is unique in its approach, as it encrypts a counter value rather than the actual plaintext or an initialization vector (IV). The encrypted counter output is then used as a keystream, which is XOR-ed with the plaintext to produce the ciphertext. This counter is typically a sequence number that is incremented for each block of plaintext.
Counter (CTR) mode, a versatile encryption method in symmetric cryptography, operates by combining the principles of block ciphers with the characteristics of stream ciphers. The technical process begins with the generation of a counter value for each block or segment of data. This counter, typically a sequence number that increases for each block, is combined with a nonce, a unique random or pseudorandom number generated for each encryption session. The nonce and counter values are concatenated and formatted into a block, matching the size of the block cipher being used. This block, rather than the plaintext itself, is then encrypted using the secret key and block cipher algorithm.
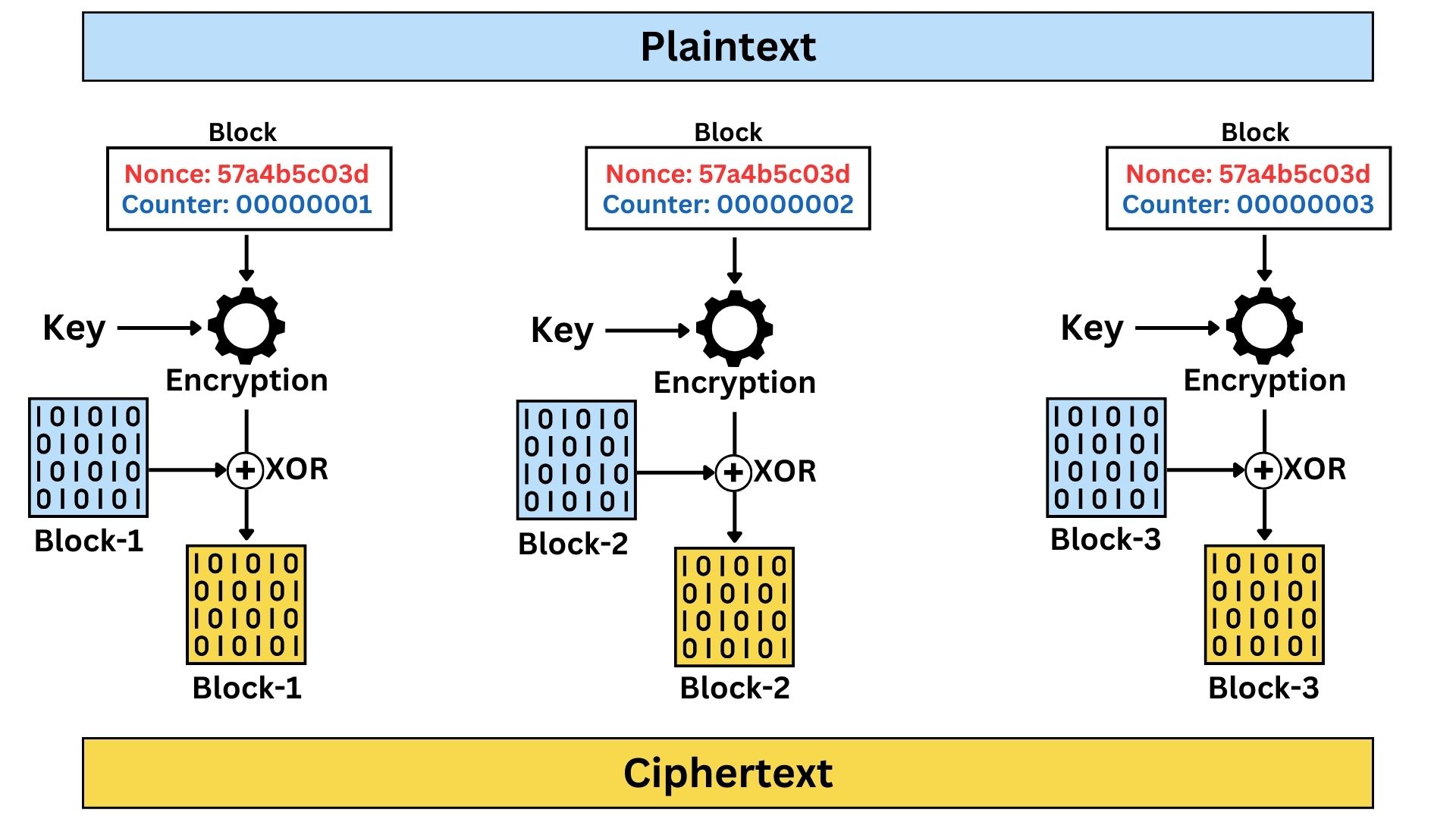
The resulting encrypted block, now a keystream, is XORed with the plaintext. This XOR operation can be applied to plaintext data organized either as fixed-size blocks or as a continuous stream. This flexibility allows CTR mode to encrypt data of any length, adapting to both block and streaming data scenarios. The output ciphertext mirrors the input plaintext format, meaning if the plaintext is processed as a block, the ciphertext is in blocks; if the plaintext is processed in a streaming manner, the ciphertext is a stream.
In decryption, the same nonce and counter values are used to regenerate the keystream. The ciphertext is then XORed with this keystream to recover the original plaintext. The key aspect of CTR mode is that the encryption and decryption processes are symmetric, relying on the generation of an identical keystream. The critical requirement for security in CTR mode is ensuring that the combination of nonce and counter is never reused under the same encryption key, as this would compromise the security of the encrypted data.
Someone might choose the Counter (CTR) mode over other encryption modes for several reasons:
- CTR mode allows for parallel processing of data blocks, significantly increasing encryption and decryption speeds, especially in hardware implementations. This is a notable advantage over modes like CBC, which require sequential processing.
- CTR can handle data of any size without needing padding, making it versatile for various applications, including those with streaming data.
- It allows random access to encrypted data, enabling decryption of specific blocks without needing to process preceding ones.
- The mode’s straightforward implementation and the lack of a need for complex padding schemes make it efficient and easy to use.
- Unlike some modes, errors in a ciphertext block in CTR mode only affect the decryption of that specific block and do not propagate to subsequent blocks, enhancing error resilience.
As we explore the nuances of Block Cipher Modes of Operation, the following comparison table will guide you through their key differences. Each mode has distinct characteristics regarding data processing, error propagation, and requirements like padding. This table will help you understand these modes better, enhancing your grasp of their applications and limitations.
| Criteria | Stream Cipher | Block Cipher |
|---|---|---|
| Data Processing | Encrypts data bit by bit or byte by byte in a continuous stream. | Encrypts data in fixed-size blocks (e.g., 64 or 128 bits). |
| Speed and Efficiency | Generally faster and more efficient for real-time encryption. | Slower compared to Stream Ciphers, especially with smaller data. |
| Use Case | Ideal for streaming data like live audio/video transmissions. | Suited for encrypting large data sets or files. |
| Key Usage | Uses the same key for the entire data stream. | Uses a series of generated round keys for different data blocks. |
| Error Propagation | An error can affect subsequent encryption. | Errors typically affect only the specific block they occur in. |
| Complexity | Less complex, easier to implement in hardware. | More complex algorithms, often requiring more computational power. |
| Security | Less secure, especially if key is reused. | Generally considered more secure due to structure and complexity. |
| Flexibility in Data Length | Can handle varying lengths of data without padding. | Requires padding if data doesn’t fit the block size. |
| Examples | RC4 (now considered insecure), ChaCha20. | AES, DES, 3DES. |
Quick Quiz
Summary
In this lesson on Symmetric Key Cryptography, we went through the fundamental aspects and techniques that form the backbone of this essential field in cybersecurity.
We began by defining Symmetric Cryptography, highlighting its role in securing digital communications by using the same key for both encryption and decryption of data. Delving into its history, we traced back to ancient methods, such as the Scytale used by the Greeks, to understand the evolution of cryptographic practices.
Our exploration then took us through key cryptographic techniques: Substitution, Permutation, and Transposition. Each technique was explained with clear examples. Substitution was illustrated through the Caesar Cipher, where characters are systematically replaced. Permutation, demonstrated via the Rail Fence Cipher, involves rearranging characters based on a systematic approach. Transposition was exemplified by the Columnar Transposition, where character positions are shifted in a straightforward manner. These techniques, while basic in their individual forms, laid the groundwork for understanding more complex cryptographic methods.
We then focused on the role of XOR (Exclusive OR) in encryption, discussing its unique property of outputting a value only when the inputs differ. XOR’s choice in encryption, due to its simplicity and effectiveness, was emphasized, particularly in the context of creating unpredictable ciphertexts.
The concept of the Initialization Vector (IV) was also addressed. We clarified that the IV adds randomness to the encryption process, enhancing security, and can be transmitted in clear text.
Moving forward, we distinguished between Stream Cipher and Block Cipher. Stream Ciphers encrypt data continuously, bit by bit, ideal for real-time data processing, while Block Ciphers encrypt fixed-size blocks of data, offering a structured approach suitable for bulk data encryption. This segment highlighted the key differences and benefits of each type, illustrating their suitability for different cryptographic needs.
Finally, we dug into Block Cipher Modes of Operation, exclusive to Block Cipher algorithms. We discussed various modes, including Electronic Codebook (ECB), Cipher Block Chaining (CBC), Cipher Feedback (CFB), Output Feedback (OFB), and Counter (CTR). Each mode was compared in terms of data processing, error propagation, padding requirements, and their individual strengths and weaknesses. This comprehensive overview provided insights into how different modes adapt the block cipher’s basic functionality to suit diverse encryption scenarios.
Homework
- Investigate the history of the Enigma Machine and its role in Symmetric Key Cryptography during World War II.
- Create a simple Caesar Cipher program in a programming language of your choice to encrypt and decrypt messages.
- Examine the differences between Symmetric and Asymmetric Key Cryptography, focusing on their uses and limitations.
- Analyze the use of Symmetric Cryptography in modern secure communication apps, like WhatsApp or Signal.
- Create your own encryption algorithm using the concepts of substitution and transposition, and challenge peers to decrypt a message.
- Investigate how modern SSDs use hardware-based encryption, specifically focusing on the role of Symmetric Key Cryptography.
- Create diagrams to reverse-engineer the decryption processes for each encryption technique and mode (Substitution, Permutation, Transposition, XOR, ECB, CBC, CFB, OFB, CTR) covered in the lesson.
If you learned something new today, help us to share it to reach others seeking knowledge.
If you have any queries or concerns, please drop them in the comment section below. We strive to respond promptly and address your questions.
Thank You









